题目内容
6.已知圆C过点(1,0),(0,$\sqrt{3}$),(-3,0),则圆C的方程为x2+y2+2x-3=0.分析 根据题意,设圆的方程为x2+y2+Dx+Ey+F=0,又由圆过点的坐标,可得$\left\{\begin{array}{l}{1+D+F=0}\\{3+\sqrt{3}E+F=0}\\{9-3D+F=0}\end{array}\right.$,解可得D、E、F的值,代入圆的方程即可得答案.
解答 解:根据题意,设圆的方程为x2+y2+Dx+Ey+F=0
又由圆C过点(1,0),(0,$\sqrt{3}$),(-3,0),
则有$\left\{\begin{array}{l}{1+D+F=0}\\{3+\sqrt{3}E+F=0}\\{9-3D+F=0}\end{array}\right.$,
解可得D=2,E=0,F=-3;
即圆的方程为:x2+y2+2x-3=0;
故答案为:x2+y2+2x-3=0.
点评 本题考查圆的一般方程,需要设出圆的一般方程,借助点的坐标构造方程组,用待定系数法分析.

练习册系列答案
相关题目
11.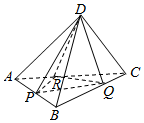 如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )
如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )
 如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )
如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )| A. | γ<α<β | B. | α<γ<β | C. | α<β<γ | D. | β<γ<α |
15.若a>b>0,且ab=1,则下列不等式成立的是( )
| A. | a+$\frac{1}{b}$<$\frac{b}{{2}^{a}}$<log2(a+b)) | B. | $\frac{b}{{2}^{a}}$<log2(a+b)<a+$\frac{1}{b}$ | ||
| C. | a+$\frac{1}{b}$<log2(a+b)<$\frac{b}{{2}^{a}}$ | D. | log2(a+b))<a+$\frac{1}{b}$<$\frac{b}{{2}^{a}}$ |
 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.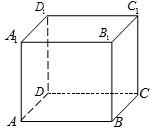 在正方体ABCD-A1B1C1D1中,给出下列结论:
在正方体ABCD-A1B1C1D1中,给出下列结论: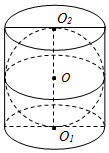 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$.
如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$.