Question

已知命题p：“存在x∈R，2x2+(m-1)x+

1

2

≤0”，命题q：“曲线C1：

x2

m2

+

y2

2m+8

=1表示焦点在x轴上的椭圆”，命题s：“曲线C2：

x2

m-t

+

y2

m-t-1

=1表示双曲线”
（1）若“p且q”是真命题，求m的取值范围；
（2）若q是s的必要不充分条件，求t的取值范围．

Answer 1

考点：必要条件、充分条件与充要条件的判断,复合命题的真假

专题：简易逻辑

分析：（1）若“p且q”是真命题，则p，q同时为真命题，建立条件关系，即可求m的取值范围；
（2）根据q是s的必要不充分条件，建立条件关系，即可求t的取值范围．

解答： 解：（1）若p为真：△=(m-1)2-4×2×

1

2

≥0…（1分）
解得m≤-1或m≥3…（2分）
若q为真：则

m2＞2m+8 2m+8＞0

…（3分）
解得-4＜m＜-2或m＞4…（4分）
若“p且q”是真命题，则

m≤-1或m≥3 -4＜m＜-2或m＞4

…（6分）
解得-4＜m＜-2或m＞4…（7分）
（2）若s为真，则（m-t）（m-t-1）＜0，即t＜m＜t+1…（8分）
由q是s的必要不充分条件，
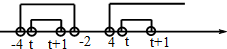
则可得{m|t＜m＜t+1}?{m|-4＜m＜-2或m＞4}…（9分）
即

t≥-4 t+1≤-2

或t≥4…（11分）
解得-4≤t≤-3或t≥4…（12分）

点评：本题主要考查充分条件和必要条件的应用，利用数轴是解决本题的关键，考查学生的推理能力．