题目内容
f(x)=
是定义在(-1,1)上的函数
(1)判断函数f(x)的奇偶性;
(2)利用函数单调性的定义证明:f(x)是其定义域上的增函数.
| x |
| 1+x2 |
(1)判断函数f(x)的奇偶性;
(2)利用函数单调性的定义证明:f(x)是其定义域上的增函数.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:证明题,函数的性质及应用
分析:(1)判断函数奇偶性时,先判断定义域是否关于原点对称,再根据定义若f(-x)=f(x),则函数为偶函数,若f(-x)=-f(x),则函数为奇函数;
(2)用定义证明函数的单调性分四步:设自变量x1,x2∈D,x1<x2--作差f(x1)-f(x2)--与0比较大小--做判断.若f(x1)<f(x2),则f(x)在D上为增函数;若f(x1)>f(x2),则f(x)在D上为减函数.
(2)用定义证明函数的单调性分四步:设自变量x1,x2∈D,x1<x2--作差f(x1)-f(x2)--与0比较大小--做判断.若f(x1)<f(x2),则f(x)在D上为增函数;若f(x1)>f(x2),则f(x)在D上为减函数.
解答:
解:(1)函数f(x)是奇函数.
∵函数的定义域为(-1,1),关于原点对称,
f(-x)=
=-f(x),
∴函数f(x)是奇函数;
(2)证明:设x1,x2∈(-1,1),且x1<x2,则
f(x1)-f(x2)=
-
=
=
,
∵-1<x1<x2<1,∴x1-x2<0,1-x1x2>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴函数f(x)在(-1,1)上是增函数.
∵函数的定义域为(-1,1),关于原点对称,
f(-x)=
| -x |
| 1+x2 |
∴函数f(x)是奇函数;
(2)证明:设x1,x2∈(-1,1),且x1<x2,则
f(x1)-f(x2)=
| x1 |
| 1+x12 |
| x2 |
| 1+x22 |
| x1(1+x22)-x2(1+x12) |
| (1+x12)(1+x22) |
| (x1-x2)(1-x1x2) |
| (1+x12)(1+x22) |
∵-1<x1<x2<1,∴x1-x2<0,1-x1x2>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴函数f(x)在(-1,1)上是增函数.
点评:本题主要考查函数的性质及应用,考查函数的奇偶性的判断和单调性的判断与证明,注意用定义证明单调性时,应严格按照步骤进行,注意变形.本题是一道基础题.

练习册系列答案
相关题目
不等式|x|(1-x2)>0的解集是( )
| A、(-1,1) |
| B、(-1,0)∪(0,1) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-∞,-1)∪(0,1) |
设a,b,c∈R,且a+b+c=2,a2+b2+c2=12,则c的最大值和最小值的差为( )
| A、2 | ||
B、
| ||
C、
| ||
D、
|
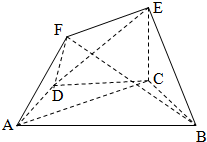 如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB= 如图,已知二次函数为y=x2,求抛物线与x=1和x轴组成的封闭图形的面积.
如图,已知二次函数为y=x2,求抛物线与x=1和x轴组成的封闭图形的面积. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,E为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,E为PD的中点.