题目内容
已知f（x）是定义在R上的奇函数，且在（0，+∞）内有1006个零点，则f（x）的零点共有（ ）
| A、1006个 |
| B、1007个 |
| C、2012个 |
| D、2013个 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数是定义在R上的奇函数，求出f（0）=0，然后由图象的对称性得到在f（x）在（-∞，0）内也有1006个零点，从而得到f（x）的零点个数．
解答：
解：∵f（x）是定义在R上的奇函数，
∴f（0）=-f（0）即f（0）=0，
∵f（x）在（0，+∞）内有1006个零点
∴由奇函数的图象关于原点对称，得，
f（x）在（-∞，0）内也有1006个零点，
∴f（x）的零点共有2013个零点．
故选D．
∴f（0）=-f（0）即f（0）=0，
∵f（x）在（0，+∞）内有1006个零点
∴由奇函数的图象关于原点对称，得，
f（x）在（-∞，0）内也有1006个零点，
∴f（x）的零点共有2013个零点．
故选D．
点评：本题主要考查奇函数的定义及图象的对称性，注意在x=0有意义，则f（0）=0，掌握对称性对于解决复杂问题很有帮助．
练习册系列答案
阅读快车系列答案
相关题目
不等式|x|（1-x2）＞0的解集是（ ）
| A、（-1，1） |
| B、（-1，0）∪（0，1） |
| C、（-∞，-1）∪（1，+∞） |
| D、（-∞，-1）∪（0，1） |
设等差数列{an}的前n项和为Sn，若S7＞S8＞S6，则满足Sn•Sn+1＜0的正整数n的值为（ ）
| A、11 | B、12 | C、13 | D、14 |
已知f（x）是定义在R上的偶函数，函数周期为2，且在区间[0，1]上是增函数，则f（-5.5）、f（-1）、f（2）的大小关系是（ ）
| A、f（-5.5）＜f（2）＜f（-1） |
| B、f（-1）＜f（-5.5）＜f（2） |
| C、f（2）＜f（-5.5）＜f（-1） |
| D、f（-1）＜f（2）＜f（-5.5） |
在直角坐标系中，直线y=
x+2的倾斜角是（ ）
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设a，b，c∈R，且a+b+c=2，a2+b2+c2=12，则c的最大值和最小值的差为（ ）
| A、2 | ||
B、
| ||
C、
| ||
D、
|
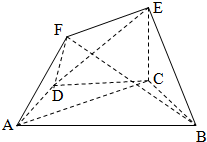如图，在多面体ABCDEF中，底面ABCD是梯形，且满足AD=DC=CB=