题目内容
7.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-4x,x<\frac{1}{2}\\{log_{\frac{1}{2}}}(2x+1),x≥\frac{1}{2}\end{array}\right.$(1)求$f(\frac{3}{2}),f({f(\frac{1}{2})})$的值;
(2)求不等式f(x)>-3的解集.
分析 (1)根据函数f(x)的解析式,分别计算f($\frac{3}{2}$)以及f(f($\frac{1}{2}$))的值即可;
(2)分别解出关于x<$\frac{1}{2}$和x≥$\frac{1}{2}$时的不等式的解集取并集即可.
解答 解:(1)f($\frac{3}{2}$)=${log}_{\frac{1}{2}}$(2×$\frac{3}{2}$+1)=${log}_{\frac{1}{2}}$4=$\frac{{log}_{2}4}{{log}_{2}\frac{1}{2}}$=-2,
f($\frac{1}{2}$)=${log}_{\frac{1}{2}}$(2×$\frac{1}{2}$+1)=${log}_{\frac{1}{2}}$2=-1,
故f(f($\frac{1}{2}$))=f(-1)=(-1)2-4×(-1)=5;
(2)x<$\frac{1}{2}$时,x2-4x>-3,解得:x<1,或x>3(舍),
故x<$\frac{1}{2}$成立,
x≥$\frac{1}{2}$时,${log}_{\frac{1}{2}}$(2x+1)>-3,
故2x+1<8,解得:x<$\frac{7}{2}$,
综上,不等式的解集是:$\left\{{x\left|{x<\frac{7}{2}}\right.}\right\}$.
点评 本题考查了函数求值问题,考查解不等式问题,是一道基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
15.某空间几何体的三视图及其尺寸如图所示,则该几何体的表面积是( )
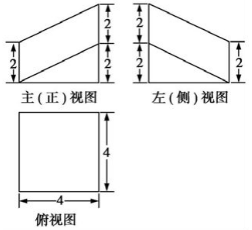

| A. | 32+8$\sqrt{6}$ | B. | 48+8$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 44+8$\sqrt{6}$ |
17.在△ABC中,D是BC中点,E是AB中点,CE交AD于点F,若$\overrightarrow{EF}=λ\overrightarrow{AB}+u\overrightarrow{AC}$,则λ+u=( )
| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $-\frac{1}{3}$ | D. | 1 |
 已知P是圆C:(x+1)2+y2=16.上任意一点,A(1,0),线段PA的垂直平分线与PC相交于点Q.
已知P是圆C:(x+1)2+y2=16.上任意一点,A(1,0),线段PA的垂直平分线与PC相交于点Q.