题目内容
下列说法中正确的个数为( )
①三角形一定是平面图形
②若四边形的两对角线相交于一点,则该四边形是平面图形
③圆心和圆上两点可确定一个平面
④三条平行线最多可确定三个平面.
①三角形一定是平面图形
②若四边形的两对角线相交于一点,则该四边形是平面图形
③圆心和圆上两点可确定一个平面
④三条平行线最多可确定三个平面.
| A、1 | B、2 | C、3 | D、4 |
考点:平面的基本性质及推论,命题的真假判断与应用
专题:简易逻辑
分析:利用确定平面的公理及其推理即可判断出.
解答:
解:①由定义可知:三角形一定是平面图形,正确.
②由相交直线确定一个平面可知:若四边形的两对角线相交于一点,则该四边形是平面图形.
③圆心和圆上两点可确定一个平面,不正确.因为当圆心和圆上两点在同一条直线上(即直径)时,此时可有无数个平面经过此三点.因此不正确.
④三条平行线最多可确定三个平面,正确.因为三棱柱的三条侧棱满足条件.
综上可知:只有①②④正确.
故选:C.
②由相交直线确定一个平面可知:若四边形的两对角线相交于一点,则该四边形是平面图形.
③圆心和圆上两点可确定一个平面,不正确.因为当圆心和圆上两点在同一条直线上(即直径)时,此时可有无数个平面经过此三点.因此不正确.
④三条平行线最多可确定三个平面,正确.因为三棱柱的三条侧棱满足条件.
综上可知:只有①②④正确.
故选:C.
点评:本题考查了确定平面的公理及其推理,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
以正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC,则双曲线的离心率为( )
A、
| ||
| B、2 | ||
C、
| ||
D、2
|
△ABC的内角A,B,C所对的边为a,b,c;则下列命题正确的是( )
①若ab>c2;则C<
②若a+b>2c;则C<
③若a3+b3=c3;则C<
④若(a+b)c<2ab;则C>
.
①若ab>c2;则C<
| π |
| 3 |
②若a+b>2c;则C<
| π |
| 3 |
③若a3+b3=c3;则C<
| π |
| 2 |
④若(a+b)c<2ab;则C>
| π |
| 2 |
| A、②③④ | B、①②③ |
| C、①②④ | D、①③④ |
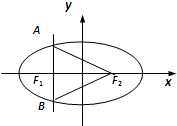 已知点F1、F2分别是椭圆
已知点F1、F2分别是椭圆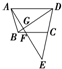 如图,梯形ABCD中,E是DC延长线上一点,AE分别交BD于G,交BC于F.则下列结论:
如图,梯形ABCD中,E是DC延长线上一点,AE分别交BD于G,交BC于F.则下列结论: