题目内容
设函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,f(x)=2x+
(x∈R).
(1)当x∈(0,1]时,求f(x)的解析式;
(2)判断f(x)在(0,1]上的单调性,并证明你的结论.
| 1 |
| x2 |
(1)当x∈(0,1]时,求f(x)的解析式;
(2)判断f(x)在(0,1]上的单调性,并证明你的结论.
考点:函数奇偶性的性质,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)根据函数奇偶性的性质即可求当x∈(0,1]时的f(x)的解析式;
(2)根据函数单调性的定义即可判断f(x)在(0,1]上的单调性.
(2)根据函数单调性的定义即可判断f(x)在(0,1]上的单调性.
解答:
解:(1)当x∈(0,1]时,-x∈[-1,0),
∵当x∈[-1,0)时,f(x)=2x+
(x∈R).
∴当-x∈[-1,0)时,f(-x)=-2x+
,
∵y=f(x)是定义在[-1,0)∪(0,1]上的奇函数,
∴f(-x)=-2x+
=-f(x),
即f(x)=2x-
,
(2)任取0<x1<x2≤1,
则f(x1)-f(x2)=2(x1-x2)+(
)2-(
)2
=2(x1-x2)+
=(x1-x2)(2+
),
∵0<x1<x2≤1,
∴x1-x2<0,2+
>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴f(x)在(0,1]上的单调递增,为增函数.
∵当x∈[-1,0)时,f(x)=2x+
| 1 |
| x2 |
∴当-x∈[-1,0)时,f(-x)=-2x+
| 1 |
| x2 |
∵y=f(x)是定义在[-1,0)∪(0,1]上的奇函数,
∴f(-x)=-2x+
| 1 |
| x2 |
即f(x)=2x-
| 1 |
| x2 |
(2)任取0<x1<x2≤1,
则f(x1)-f(x2)=2(x1-x2)+(
| 1 |
| x1 |
| 1 |
| x2 |
=2(x1-x2)+
| (x1-x2)(x1+x2) |
| x1x2 |
=(x1-x2)(2+
| x1+x2 |
| x1x2 |
∵0<x1<x2≤1,
∴x1-x2<0,2+
| x1+x2 |
| x1x2 |
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴f(x)在(0,1]上的单调递增,为增函数.
点评:本题主要考查函数奇偶性和单调性的应用,利用函数单调性的定义和奇偶性的性质是解决本题的关键.

练习册系列答案
相关题目
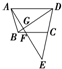 如图,梯形ABCD中,E是DC延长线上一点,AE分别交BD于G,交BC于F.则下列结论:
如图,梯形ABCD中,E是DC延长线上一点,AE分别交BD于G,交BC于F.则下列结论: