题目内容
18.一个圆锥的底面半径是4,侧面展开图为四分之一圆面,一小虫从圆锥底面圆周上一点出发绕圆锥表面一周回到原处,其最小距离为$16\sqrt{2}$.分析 根据已知,求出圆锥的母线长,进而根据小虫爬行的最小距离是侧面展开图中的弦长,可得答案.
解答 解:设圆锥的底面半径为r=4,母线长为l,
∵圆锥的侧面展开图是一个四分之一圆面,
∴2πr=$\frac{1}{2}$πl,
∴l=4r=16,
又∵小虫爬行的最小距离是侧面展开图中的弦长,
如下图所示:
故最小距离为:$16\sqrt{2}$,
故答案为:$16\sqrt{2}$.
点评 本题考查的知识点是圆锥的几何特征,空间几何的最小距离问题,难度中档.

练习册系列答案
相关题目
3.已知集合M={x|$\frac{2}{x}$≥1},N={y|y=1-x2},则M∩N=( )
| A. | (-∞,2] | B. | (0,1] | C. | (0,2] | D. | [0,1] |
7.用反证法证明“如果a<b,那么$\root{3}{a}<\root{3}{b}$”时,假设的内容应是( )
| A. | a>b | B. | $\root{3}{a}>\root{3}{b}$ | C. | $\root{3}{a}=\root{3}{b}$且$\root{3}{a}>\root{3}{b}$ | D. | $\root{3}{a}=\root{3}{b}$或$\root{3}{a}>\root{3}{b}$ |
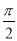 <φ<
<φ<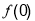 的值是 .
的值是 .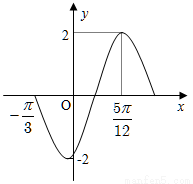
 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.