题目内容
10.一个红色的棱长是3cm的正方体,将其适当分割成棱长为1cm的小正方体,这样的小正方体共得27个,二面涂色的小正方体有12个.分析 一个红色的棱长是3cm的正方体,纵向平均切三次,横向平均切三次,侧向平均切三次,能得到27个小正方体二面涂有颜色的小正方体在棱上中间位置,由此能求出结果.
解答 解:一个红色的棱长是3cm的正方体,将其适当分割成棱长为1cm的小正方体,
纵向平均切三次,横向平均切三次,侧向平均切三次,
一共能得到27个这样的小正方体,
在27个小正方体中,恰好有三个面都涂色有颜色的共有8个,
恰好有两个都涂有颜色的共12个,恰好有一个面都涂有颜色的共6个,表面没涂颜色的1个.
故答案为:27,12.
点评 本题考查满足条件的小正方体的个数的求法,是基础题,解题时要认真审题,注意正方体结构特征的合理运用.

练习册系列答案
相关题目
5.观察下面的几何体,哪些是棱柱( )


| A. | ①③⑤ | B. | ①⑥ | C. | ①③⑥ | D. | ③④⑥ |
 .
. 在点
在点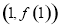 处的切线方程为
处的切线方程为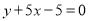 ,求函数
,求函数 是函数
是函数 ,求
,求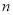 的值;
的值; 时,函数
时,函数 ,且
,且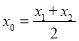 ,求证:
,求证: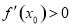 .
.