题目内容
13. 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.(Ⅰ)求证:DE是圆O的切线;
(Ⅱ)求证:DE•BC=DM•AC+DM•AB.
分析 (Ⅰ)连接BE,OE,由已知得∠ABC=90°=∠AEB,∠A=∠A,从而△AEB∽△ABC,进而∠ABE=∠C,进而∠BEO+∠DEB=∠DCE+∠CBE=90°,由此能证明DE是圆O的切线.
(Ⅱ)DM=OD-OM=$\frac{1}{2}$(AC-AB),从而DM•AC+DM•AB=$\frac{1}{2}$(AC-AB)•(AC+AB)=$\frac{1}{2}$BC2,由此能证明DE•BC=DM•AC+DM•AB.
解答 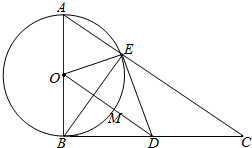 证明:(Ⅰ)连接BE,OE,
证明:(Ⅰ)连接BE,OE,
∵AB是直径,∴∠AEB=90°,
∵∠ABC=90°=∠AEB,∠A=∠A,∴△AEB∽△ABC,
∴∠ABE=∠C,
∵BE⊥AC,D为BC的中点,∴DE=BD=DC,
∴∠DEC=∠DCE=∠ABE=∠BEO,∠DBE=∠DEB,
∴∠BEO+∠DEB=∠DCE+∠CBE=90°,
∴∠OED=90°,∴DE是圆O的切线.
(Ⅱ)证明:∵O、D分别为AB、BC的中点,
∴DM=OD-OM=$\frac{1}{2}$(AC-AB),
∴DM•AC+DM•AB
=DM•(AC+AB)
=$\frac{1}{2}$(AC-AB)•(AC+AB)
=$\frac{1}{2}$(AC2-AB2)
=$\frac{1}{2}$BC2
=DE•BC.
∴DE•BC=DM•AC+DM•AB.
点评 本题考查DE是圆O的切线的证明,考查DE•BC=DM•AC+DM•AB的证明,是中档题,解题时要认真审题,注意弦切角定理的合理运用.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
10.数列{an}的通项an=n2(cos2$\frac{nπ}{3}$-sin2$\frac{nπ}{3}$),其前n项和为Sn,则S29为( )
| A. | -430 | B. | -470 | C. | 470 | D. | 490 |
5.观察下面的几何体,哪些是棱柱( )


| A. | ①③⑤ | B. | ①⑥ | C. | ①③⑥ | D. | ③④⑥ |
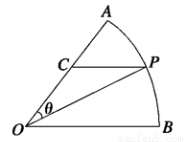
 ,圆心角
,圆心角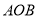 的大小等于
的大小等于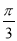 ,半径为
,半径为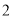 百米,在半径
百米,在半径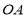 上取一点
上取一点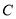 ,过点
,过点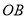 的直线交弧
的直线交弧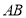 于点
于点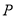 .设
.设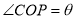 .
.
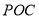 面积
面积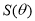 的函数表达式.
的函数表达式.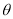 的值.
的值.