题目内容
3.已知集合M={x|$\frac{2}{x}$≥1},N={y|y=1-x2},则M∩N=( )| A. | (-∞,2] | B. | (0,1] | C. | (0,2] | D. | [0,1] |
分析 求出M中不等式的解集确定出M,求出N中y的范围确定出N,找出M与N的交集即可.
解答 解:由M中不等式$\frac{2}{x}$≥1,解得:0<x≤2,即M=(0,2],
由N中y=1-x2≤1,得到N=(-∞,1],
则M∩N=(0,1],
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
8.不等式|x-3|<2的解集是( )
| A. | {x|x>5或x<1} | B. | {x|1<x<5} | C. | {x|-5<x<-1} | D. | {x|x>1} |
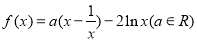 ,
,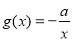 ,若至少存在一个
,若至少存在一个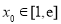 ,使
,使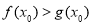 成立,则实数a的范围为( )
成立,则实数a的范围为( )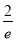 ,+∞) B.(0,+∞)
,+∞) B.(0,+∞) 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 是函数
是函数 的极小值点,则
的极小值点,则 =( )
=( )