题目内容
 y=f(x)是定义在[-3,3]的偶函数,当x∈[0,1]时,y=f(x)的图象是y=x2在相应区间上的部分(如图所示);当x∈(1,3]时,y=f(x)的图象是一次函数y=-x+3在相应区间上的部分.
y=f(x)是定义在[-3,3]的偶函数,当x∈[0,1]时,y=f(x)的图象是y=x2在相应区间上的部分(如图所示);当x∈(1,3]时,y=f(x)的图象是一次函数y=-x+3在相应区间上的部分.(1)求f(-
| 1 |
| 2 |
(2)画出其图象并写出其单调区间;
(3)写出函数y=f(x)的表达式(用两种方法解答).
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)结合已知条件直接求出f(-
)、f(-1)、f(-2)、f(-3)的值.
(2)根据函数f(x)是定义在[-3,3]上的偶函数,可得函数的图象关于y轴对称,根据对称性,可得f(x)在y轴右侧的图象;写出其单调区间;
(2)利用函数的性质求出函数的表达式,方法一是利用图象的对称性;二是,函数偶函数的性质求解.
| 1 |
| 2 |
(2)根据函数f(x)是定义在[-3,3]上的偶函数,可得函数的图象关于y轴对称,根据对称性,可得f(x)在y轴右侧的图象;写出其单调区间;
(2)利用函数的性质求出函数的表达式,方法一是利用图象的对称性;二是,函数偶函数的性质求解.
解答:
解:(1)y=f(x)是定义在[-3,3]的偶函数,当x∈[0,1]时,y=f(x)的图象是y=x2在相应区间上的部分(如图所示);当x∈(1,3]时,y=f(x)的图象是一次函数y=-x+3在相应区间上的部分.
∴f(-
)=f(
)=
;
f(-1)=f(1)=1;
f(-2)=f(2)=-2+3=1;
f(-3)=f(3)=-3+3=0.
(2)∵函数f(x)是定义在[-3,3]上的偶函数,∴函数的图象关于y轴对称,根据对称性,可得f(x)在y轴右侧的图象,如图所示: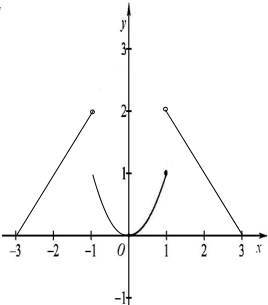
函数的单调增区间是:[-3,-1],(0,1);单调减区间是:(-1,0],[1,3].
(3)方法一:由函数图象的对称性可知,当x∈[-1,0]时,函数y=x2;当x∈[-3,-1)时,f(x)=x+3.
即f(x)=
.
方法二:∵函数是偶函数,当x∈[-1,0]时,-x∈[0,1],函数y=(-x)2=x2;
当x∈[-3,-1)时,-x∈(1,3],f(x)=-(-x)+3=x+3.
∴f(x)=
.
∴f(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
f(-1)=f(1)=1;
f(-2)=f(2)=-2+3=1;
f(-3)=f(3)=-3+3=0.
(2)∵函数f(x)是定义在[-3,3]上的偶函数,∴函数的图象关于y轴对称,根据对称性,可得f(x)在y轴右侧的图象,如图所示:

函数的单调增区间是:[-3,-1],(0,1);单调减区间是:(-1,0],[1,3].
(3)方法一:由函数图象的对称性可知,当x∈[-1,0]时,函数y=x2;当x∈[-3,-1)时,f(x)=x+3.
即f(x)=
|
方法二:∵函数是偶函数,当x∈[-1,0]时,-x∈[0,1],函数y=(-x)2=x2;
当x∈[-3,-1)时,-x∈(1,3],f(x)=-(-x)+3=x+3.
∴f(x)=
|
点评:本题考查偶函数图象的对称性,考查数形结合的数学思想,考查学生的作图能力.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
如果复数z=
(a是实数)的实部为1,则z的虚部为为( )
| a+i |
| 1-i |
| A、1 | B、-1 | C、2 | D、-2 |
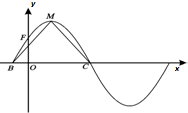 将函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象向右平移
将函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象向右平移