题目内容
设函数f(x)在R上单调递减,且对于任意实数m,n,总有f(m+n)=f(m)•f(n),设A={(x,y)|f(x2)•f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=∅,则a的取值范围是( )
A、-
| ||||
B、-
| ||||
C、0≤a≤
| ||||
D、-
|
考点:交集及其运算
专题:集合
分析:令n=0,代入f(m+n)=f(m)•f(n),可得出f(0)=1,根据A与B的交集为空集,得到圆心(0,0)到直线的距离d大于等于半径1,即可确定出a的范围.
解答:
解:令n=0,得到f(m+0)=f(m)f(0)对于任意实数m恒成立,故f(0)=1,
∵f(x2)•f(y2)>f(1),f(ax-y+2)=1,
∴x2+y2<1,ax-y+2=0,
∵A∩B=∅,
∴圆心(0,0)到直线的距离应满足d=
≥1,
解得:-
≤a≤
.
故选:A.
∵f(x2)•f(y2)>f(1),f(ax-y+2)=1,
∴x2+y2<1,ax-y+2=0,
∵A∩B=∅,
∴圆心(0,0)到直线的距离应满足d=
| 2 | ||
|
解得:-
| 3 |
| 3 |
故选:A.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
已知x、y满足条件
,若目标函数z=ax+y取得最大值时的最优解有无数个,则实数a的值为( )
|
A、-
| ||
B、-
| ||
C、
| ||
D、
|
在数列{an}中,a1=1,a2=2,且an+2-an=1+(-1)n(n∈N*),则S100=( )
| A、2100 | B、2600 |
| C、2800 | D、3100 |
函数y=x2(x≤0)的反函数是( )
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
为了得到函数y=cos2x(x∈R)的图象只需将函数y=cos(2x+
)(x∈R)的图象( )
| π |
| 3 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
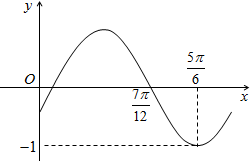
已知函数y=sin(ωx+φ)(ω>0,-
<φ<
)的部分图象如图所示,则( )
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=-
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=-
| ||
D、ω=1,φ=
|
已知集合A={x∈Z|x2-2x≤0},集合B={x|x=2a,a∈A},则A∩B为( )
| A、{0} | B、{2} |
| C、{0,2} | D、{1,4} |
若x,y满足约束条件
,则z=2x+y的最小值是( )
|
| A、-1 | B、0 | C、2 | D、8 |
| 3 | a2 |
|
A、a
| ||
B、a
| ||
C、a
| ||
D、a
|