题目内容
已知集合A={m|m=n2-4n+5}，B={n|m=
}，求A∩B，A∪B．
| 5-n |
考点：并集及其运算,交集及其运算
专题：集合
分析：求出A中m的范围确定出A，求出B中n的范围确定出B，求出A与B的交集及并集即可．
解答：
解：由A中m=n2-4n+5=（n-2）2+1≥1，
得到A=[1，+∞），
由B中m=
，得到5-n≥0，
解得：n≤5，即B=（-∞，5]，
则A∩B=[1，5]，A∪B=R．
得到A=[1，+∞），
由B中m=
| 5-n |
解得：n≤5，即B=（-∞，5]，
则A∩B=[1，5]，A∪B=R．
点评：此题考查了并集及其运算，以及交集及其运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
在边长为1的等边三角形ABC中，
•
=（ ）
| AB |
| AC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
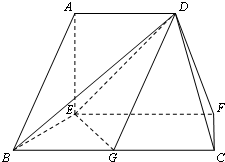在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC，
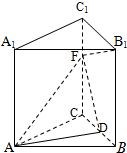在直三棱柱ABC-A1B1C1中，AB=AC=AA1=3a，BC=2a，D是BC的中点，F是C1C上一点，且CF=2a．
已知：如图AD，BC，AE分别是⊙O的三条切线，切点分别是D，E，F，AG是⊙O的一条割线，交⊙O于F，G两点，△ABC的周长2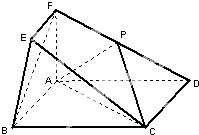
在如图所示的几何体中，四边形ABCD为矩形，平面ABEF⊥平面ABCD，EF∥AB，∠BAF=90°，AD=2，AB=AF=2EF=1，点P在棱DF上．
如图，四棱锥A-BCDE，平面ABC⊥平面BCDE，△ABC边长为2的等边三角形，底面BCDE是矩形，且CD=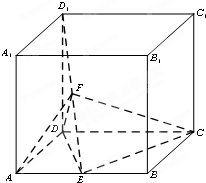
如图，四棱柱ABCD-A1B1C1D1中，DD1⊥底面ABCD．ABCD为平行四边形，∠DAB=60°，AB=2AD=2．DD1=3，E，F分别是AB与D1E的中点．