题目内容
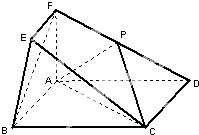 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.(1)若P为DF的中点,求证:BF∥平面ACP
(2)若直线PC与平面FAD所成角的正弦值为
| 2 |
| 3 |
考点:直线与平面平行的判定,平面与平面垂直的性质
专题:空间位置关系与距离
分析:(1)连接BD,交AC于点O,连接OP.利用OP为三角形BDF中位线,可得BF∥OP,利用线面平行的判定,可得BF∥平面ACP;
(2)由已知中平面ABEF⊥平面ABCD,由面面垂直的性质定理可得AF⊥平面ABCD,进而AF⊥CD,结合四边形ABCD为矩形及线面垂直的判定定理,可得CD⊥平面FAD,故∠CPD就是直线PC与平面FAD所成角,进而解三角形求出DF和PD,进而可得PF的长度.
(2)由已知中平面ABEF⊥平面ABCD,由面面垂直的性质定理可得AF⊥平面ABCD,进而AF⊥CD,结合四边形ABCD为矩形及线面垂直的判定定理,可得CD⊥平面FAD,故∠CPD就是直线PC与平面FAD所成角,进而解三角形求出DF和PD,进而可得PF的长度.
解答:
 证明:(1)连接BD,交AC于点O,连接OP.
证明:(1)连接BD,交AC于点O,连接OP.
∵P是DF中点,O为矩形ABCD对角线的交点,
∴OP为三角形BDF中位线,…(3分)
∴BF∥OP,
又∵BF?平面ACP,OP?平面ACP,
∴BF∥平面ACP. …(6分)
解:(2)∵∠BAF=90°,
∴AF⊥AB,
又∵平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,
∴AF⊥平面ABCD,…(8分)
∴AF⊥CD
∵四边形ABCD为矩形
∴AD⊥CD …(10分)
又∵AF∩AD=A,AF,AD?平面FAD
∴CD⊥平面FAD
∴∠CPD就是直线PC与平面FAD所成角…(12分)
∴sin∠CPD=
,
又∵AD=2,AB=CD=AF=1,
∴DF=
=
,PD=
=
=
,
∴得PF=DF-PD=
…(14分)
 证明:(1)连接BD,交AC于点O,连接OP.
证明:(1)连接BD,交AC于点O,连接OP.∵P是DF中点,O为矩形ABCD对角线的交点,
∴OP为三角形BDF中位线,…(3分)
∴BF∥OP,
又∵BF?平面ACP,OP?平面ACP,
∴BF∥平面ACP. …(6分)
解:(2)∵∠BAF=90°,
∴AF⊥AB,
又∵平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,
∴AF⊥平面ABCD,…(8分)
∴AF⊥CD
∵四边形ABCD为矩形
∴AD⊥CD …(10分)
又∵AF∩AD=A,AF,AD?平面FAD
∴CD⊥平面FAD
∴∠CPD就是直线PC与平面FAD所成角…(12分)
∴sin∠CPD=
| 2 |
| 3 |
又∵AD=2,AB=CD=AF=1,
∴DF=
| AD2+AF2 |
| 5 |
| PC2-CD2 |
(
|
| ||
| 2 |
∴得PF=DF-PD=
| ||
| 2 |
点评:本题考查线面平行,考查线面夹角,其中(2)的关键是证明∠CPD就是直线PC与平面FAD所成角.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
下列函数中,最小正周期是
的偶函数为( )
| π |
| 2 |
| A、y=tan2x | ||
B、y=cos(4x+
| ||
| C、y=2cos22x-1 | ||
| D、y=cos2x |
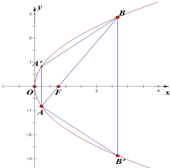 在平面直角坐标系xOy中,抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1.
在平面直角坐标系xOy中,抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1.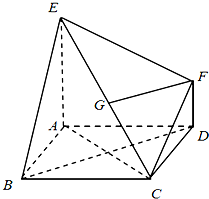 如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.
如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.