题目内容
 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,
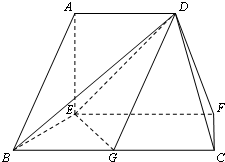
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求三棱锥A-BED的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)先证明出AB∥DG,即而根据线面平行的判定定理证明出AB∥平面DEG.
(2)先根据线面垂直的性质证明出EF⊥AE,进而根据线面垂直的判定定理证明出AE⊥平面BCFE,根据线面垂直的性质推断出DH⊥EG,证明出四边形BGHE为正方形,进而推断出BH⊥EG,最后根据线面垂直的判定定理证明出EG⊥平面BHD,则BD⊥EG得证.
(3)先证明出AD⊥平面AEB,推断出三棱锥A-BED的高为AD,进而根据三棱锥体积的公式求得其体积.
(2)先根据线面垂直的性质证明出EF⊥AE,进而根据线面垂直的判定定理证明出AE⊥平面BCFE,根据线面垂直的性质推断出DH⊥EG,证明出四边形BGHE为正方形,进而推断出BH⊥EG,最后根据线面垂直的判定定理证明出EG⊥平面BHD,则BD⊥EG得证.
(3)先证明出AD⊥平面AEB,推断出三棱锥A-BED的高为AD,进而根据三棱锥体积的公式求得其体积.
解答:
 (1)证明:∵AD∥EF,EF∥BC,∴AD∥BC.
(1)证明:∵AD∥EF,EF∥BC,∴AD∥BC.
又∵BC=2AD,G是BC的中点,∴AD∥BG,
∴四边形ADGB是平行四边形,∴AB∥DG.
又∵AB?平面DEG,DG?平面DEG,∴AB∥平面DEG.
(2)证明:∵EF⊥平面AEB,AE?平面AEB,∴EF⊥AE,
又AE⊥EB,EB∩EF=E,EB,EF?平面BCFE,∴AE⊥平面BCFE.
过D作DH∥AE交EF于H,则DH⊥平面BCFE.
∵EG?平面BCFE,∴DH⊥EG.
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,∴EH=AD=2,
∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,∴BH⊥EG,
又BH∩DH=H,BH?平面BHD,DH?平面BHD,∴EG⊥平面BHD.
∵BD?平面BHD,∴BD⊥EG.
(3)∵EF⊥平面AEB,EF∥AD,∴AD⊥平面AEB,故三棱锥A-BED的高为AD
∵AE⊥EB,∴S△AEB=
AE•BE=
×2×2=2,
∴VA-BED=
AD•S△AEB=
×2×2=
.
 (1)证明:∵AD∥EF,EF∥BC,∴AD∥BC.
(1)证明:∵AD∥EF,EF∥BC,∴AD∥BC.又∵BC=2AD,G是BC的中点,∴AD∥BG,
∴四边形ADGB是平行四边形,∴AB∥DG.
又∵AB?平面DEG,DG?平面DEG,∴AB∥平面DEG.
(2)证明:∵EF⊥平面AEB,AE?平面AEB,∴EF⊥AE,
又AE⊥EB,EB∩EF=E,EB,EF?平面BCFE,∴AE⊥平面BCFE.
过D作DH∥AE交EF于H,则DH⊥平面BCFE.
∵EG?平面BCFE,∴DH⊥EG.
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,∴EH=AD=2,
∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,∴BH⊥EG,
又BH∩DH=H,BH?平面BHD,DH?平面BHD,∴EG⊥平面BHD.
∵BD?平面BHD,∴BD⊥EG.
(3)∵EF⊥平面AEB,EF∥AD,∴AD⊥平面AEB,故三棱锥A-BED的高为AD
∵AE⊥EB,∴S△AEB=
| 1 |
| 2 |
| 1 |
| 2 |
∴VA-BED=
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题主要考查了线面平行,线面垂直的判定定理的运用.要求学生对基础定理能熟练记忆并灵活运用.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
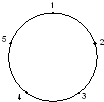 如图,圆周上按顺时针方向标有1,2,3,4,5五个点.一只青蛙按顺时针方向绕圆从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则跳两个点.该青蛙从5这点跳起,经2013次跳后它将停在的点是( )
如图,圆周上按顺时针方向标有1,2,3,4,5五个点.一只青蛙按顺时针方向绕圆从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则跳两个点.该青蛙从5这点跳起,经2013次跳后它将停在的点是( )| A、1 | B、2 | C、3 | D、4 |
 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′-DEF的体积最大值为
| 1 |
| 64 |
④存在某个位置,使得DF与A′E垂直.
其中正确的命题是( )
| A、② | B、②③ |
| C、①②③ | D、①②③④ |
归纳推理是( )
| A、特殊到一般的推理 |
| B、特殊到特殊的推理 |
| C、一般到特殊的推理 |
| D、一般到一般的推理 |
如图,该程序运行后的输出结果为( )


| A、0 | B、3 | C、12 | D、-2 |
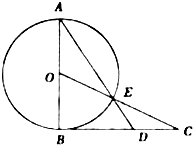 如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D. 如图,在△ABC中,AB=4,AC=1,∠BAC=60°.
如图,在△ABC中,AB=4,AC=1,∠BAC=60°.