题目内容
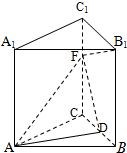 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.(1)求证:B1F⊥平面ADF;
(2)求C点到平面AFD的距离;
(3)试在棱AA1上找一点E,使得BE∥平面ADF.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)证明B1F⊥平面ADF,只需证明B1F⊥AF,AD⊥B1F;
(2)利用等体积,可求C点到平面AFD的距离;
(3)当AE=2a时,BE∥平面ADF,再进行证明即可.
(2)利用等体积,可求C点到平面AFD的距离;
(3)当AE=2a时,BE∥平面ADF,再进行证明即可.
解答:
(1)证明:∵AB=AC,D为BC中点∴AD⊥BC
又在直三棱柱中,BB1⊥底面ABC,
AD?底面ABC,
∴AD⊥BB1,∴AD⊥平面BCC1B1,…2′
∵B1F?平面BCC1B1
∴AD⊥B1F,在矩形BCC1B1中,C1F=CD=a,CF=C1B1=2a,
∴Rt△DCFRt≌△FC1B1,…5′
∴∠CFD=∠C1B1F,∴∠B1FD=90°,即B1F⊥FD
∵AD∩FD=D,∴B1F⊥平面AFD…6′
(2)解:AD=2
a, 且AD⊥平面BB1C1C
∴AD⊥DF,DF=
a
∴S△ADF=
a2,S△ACD=
a2
∵Vc-AFD=VF-ACD…15′
∴h=
a…9′
(3)解:当AE=2a时,BE∥平面ADF.
证明:连EF,EC,设EC∩AF=M,
连DM,∵AE=CF=2a,
∴AEFC为矩形,
∴M为EC中点,∵D为BC中点,…13′
∴MD∥BE,∵MD?平面ADF,
BE?平面ADF,∴BE∥平面ADF.…16′
又在直三棱柱中,BB1⊥底面ABC,
AD?底面ABC,
∴AD⊥BB1,∴AD⊥平面BCC1B1,…2′
∵B1F?平面BCC1B1
∴AD⊥B1F,在矩形BCC1B1中,C1F=CD=a,CF=C1B1=2a,
∴Rt△DCFRt≌△FC1B1,…5′
∴∠CFD=∠C1B1F,∴∠B1FD=90°,即B1F⊥FD
∵AD∩FD=D,∴B1F⊥平面AFD…6′
(2)解:AD=2
| 2 |
∴AD⊥DF,DF=
| 5 |
∴S△ADF=
| 10 |
| 2 |
∵Vc-AFD=VF-ACD…15′
∴h=
2
| ||
| 5 |
(3)解:当AE=2a时,BE∥平面ADF.
证明:连EF,EC,设EC∩AF=M,
连DM,∵AE=CF=2a,
∴AEFC为矩形,
∴M为EC中点,∵D为BC中点,…13′
∴MD∥BE,∵MD?平面ADF,
BE?平面ADF,∴BE∥平面ADF.…16′
点评:本题考查线面平行、线面垂直,考查点面距离,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知
=
,则tanθ=( )
| 1+sinθ+cosθ |
| 1+sinθ-cosθ |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
归纳推理是( )
| A、特殊到一般的推理 |
| B、特殊到特殊的推理 |
| C、一般到特殊的推理 |
| D、一般到一般的推理 |
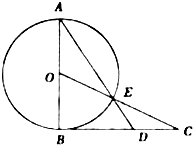 如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.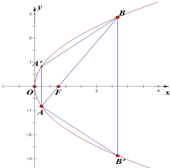 在平面直角坐标系xOy中,抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1.
在平面直角坐标系xOy中,抛物线y2=2px上一点到焦点F的距离与到y轴的距离的差为1.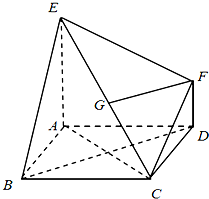 如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.
如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.