题目内容
3.已知抛物线y2=2px(p>0)的焦点成F,过点F且倾斜角为45°的直线l与抛物线在第一、第四象限分别交于A、B,则$\frac{|AF|}{|BF|}$等于( )| A. | 3 | B. | 7+4$\sqrt{3}$ | C. | 3+2$\sqrt{2}$ | D. | 2 |
分析 直线l的方程为y=x-$\frac{p}{2}$,代入y2=2px,整理得4x2-12px+p2=0,解得x=$\frac{3±2\sqrt{2}}{2}$p,即可求出$\frac{|AF|}{|BF|}$.
解答 解:直线l的方程为y=x-$\frac{p}{2}$,代入y2=2px,整理得4x2-12px+p2=0,解得x=$\frac{3±2\sqrt{2}}{2}$p,
∴$\frac{|AF|}{|BF|}$=$\frac{2+\sqrt{2}}{2-\sqrt{2}}$=3+2$\sqrt{2}$.
故选C.
点评 本题考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.在△ABC中,$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{DC}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且则$\overrightarrow{AD}$=( )
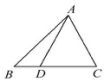

| A. | $\frac{4}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
18.函数f(x)=x2-5x+6,x∈[-5,5],在定义域内任取一点x0,使f(x0)≤0的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{4}{5}$ |
8.将号码分别为1、2、3、4的四个小球放入一个袋中,这些小球仅号码不同,其余完全相同.甲从袋中摸出一个球,号码为a,放回后,乙从此袋再摸出一个球,其号码为b,则使不等式a>2b-2成立的事件发生的概率等于( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
12.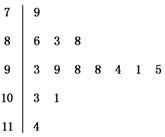 如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
 如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )| A. | 98 | B. | 94 | C. | 94.5 | D. | 95 |
13.函数f(x)=x+cosx在[0,π]上的最小值为( )
| A. | -2 | B. | 0 | C. | -$\frac{1}{2}$ | D. | 1 |