题目内容
18．函数f（x）=x2-5x+6，x∈[-5，5]，在定义域内任取一点x0，使f（x0）≤0的概率是（ ）| A． | $\frac{1}{10}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{10}$ | D． | $\frac{4}{5}$ |
分析 首先求出f（x0）≤0的x0的范围，利用区间长度的比求概率．
解答 解：函数f（x）=x2-5x+6=（x-2）（x-3），x∈[-5，5]，
在定义域内任取一点x0，使f（x0）≤0的x0的范围是[2，3]，
由几何概型的公式得到使f（x0）≤0的概率是$\frac{3-2}{5-（-5）}=\frac{1}{10}$；
故选：A．
点评 本题考查了几何概型的概率问题；关键是明确几何测度，利用几何概型的公式解答．
练习册系列答案
相关题目
19．函数y=x2在P（1，1）处的切线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线平行，则双曲线的离心率是（ ）
| A． | 5 | B． | $\sqrt{5}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{3}$ |
3．已知抛物线y2=2px（p＞0）的焦点成F，过点F且倾斜角为45°的直线l与抛物线在第一、第四象限分别交于A、B，则$\frac{|AF|}{|BF|}$等于（ ）
| A． | 3 | B． | 7+4$\sqrt{3}$ | C． | 3+2$\sqrt{2}$ | D． | 2 |
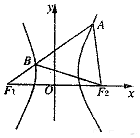如图，F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点，过F1的直线l与双曲线分别交于点A，B，且A（1，$\sqrt{3}$），若△ABF2为等边三角形，则△BF1F2的面积为（ ）