题目内容
8.将号码分别为1、2、3、4的四个小球放入一个袋中,这些小球仅号码不同,其余完全相同.甲从袋中摸出一个球,号码为a,放回后,乙从此袋再摸出一个球,其号码为b,则使不等式a>2b-2成立的事件发生的概率等于( )| A. | $\frac{3}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 基本事件总数n=4×4=16,再用列举法求出使不等式a>2b-2成立的基本事件个数,由此能求出使不等式a>2b-2成立的事件发生的概率.
解答 解:将号码分别为1、2、3、4的四个小球放入一个袋中,这些小球仅号码不同,其余完全相同.
甲从袋中摸出一个球,号码为a,放回后,乙从此袋再摸出一个球,其号码为b,
则基本事件总数n=4×4=16,
要使不等式a>2b-2成立,
则当a=1时,b=1;
当a=2时,b=1;
当a=3时,b=1,2;
当a=4时,b=1,2.
故满足a>2b-1的基本事件共有m=6个,
∴使不等式a>2b-2成立的事件发生的概率为p=$\frac{m}{n}=\frac{6}{16}=\frac{3}{8}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
3.已知抛物线y2=2px(p>0)的焦点成F,过点F且倾斜角为45°的直线l与抛物线在第一、第四象限分别交于A、B,则$\frac{|AF|}{|BF|}$等于( )
| A. | 3 | B. | 7+4$\sqrt{3}$ | C. | 3+2$\sqrt{2}$ | D. | 2 |
20.若m<n,p<q,且(p-m)(p-n)<0,(q-m)(q-n)<0,则m,n,p,q从小到大排列顺序是( )
| A. | m<p<q<n | B. | p<m<q<n | C. | m<p<n<q | D. | p<m<n<q |
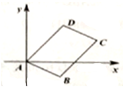 如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.
如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.