题目内容
已知函数y=ax(a>0且a≠1)在[1,2]上的最大值与最小值之和为6,记f(x)=
.
(1)求a的值;
(2)判断函数f(x)的奇偶性;
(3)求不等式f(x)>
的解集.
| ax-1 |
| ax+1 |
(1)求a的值;
(2)判断函数f(x)的奇偶性;
(3)求不等式f(x)>
| 15 |
| 17 |
考点:函数的最值及其几何意义,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)利用指数函数的单调性的性质利用函数最值之和为6,建立方程即可求a的值;
(2)根据函数的奇偶性的定义即可判断函数f(x)的奇偶性;
(3)结合指数函数的性质即可解不等式f(x)>
的解集.
(2)根据函数的奇偶性的定义即可判断函数f(x)的奇偶性;
(3)结合指数函数的性质即可解不等式f(x)>
| 15 |
| 17 |
解答:
解:(1)∵函数y=ax在[1,2]上的最大值与最小值之和为6,
∴a+a2=6…(3分)
得a=2,或a=-3(舍去) …(4分)
(2)f(x)=
,定义域为R…(5分)
f(-x)=
=
=
=-f(x)…(8分)
∴函数f(x)为奇函数…(9分)
(3)∵f(x)>
,∴
>
化简得2x>16…(11分)
解得x>4…(13分)
∴不等式f(x)>
的解集为{x|x>4}…(14分)
∴a+a2=6…(3分)
得a=2,或a=-3(舍去) …(4分)
(2)f(x)=
| 2x-1 |
| 2x+1 |
f(-x)=
| 2-x-1 |
| 2-x+1 |
| ||
|
| 1-2x |
| 1+2x |
∴函数f(x)为奇函数…(9分)
(3)∵f(x)>
| 15 |
| 17 |
| 2x-1 |
| 2x+1 |
| 15 |
| 17 |
化简得2x>16…(11分)
解得x>4…(13分)
∴不等式f(x)>
| 15 |
| 17 |
点评:本题主要考查指数函数的图象和性质,结合条件求出a的值是解决本题的关键.

练习册系列答案
相关题目
对任意x,y∈R,函数f(x)都满足f(x+y)=f(x)+f(y)+2恒成立,则f(5)+f(-5)等于( )
| A、0 | B、-4 | C、-2 | D、2 |
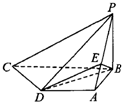 如图所示,四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA,则平面ABE与平面BED的夹角的余弦值为
如图所示,四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA,则平面ABE与平面BED的夹角的余弦值为