题目内容

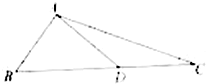
如图，在△ABC中，AD⊥AB，
BC
=
3
BD
，|
AD
|=1，则
AC
•
AD
=
 
．
考点：平面向量数量积的运算
专题：计算题,解三角形,平面向量及应用
分析：运用向量的数量积的定义，结合条件可得
AC
•
AD
=|
AC
|cos∠DAC，再由诱导公式可得
AC
•
AD
=|
AC
|sin∠BAC，结合三角形ABC中的正弦定理和直角三角形的锐角三角函数的定义，计算即可得到所求值．
解答： 解：
AC
•
AD
=|
AC
|•|
AD
|cos∠DAC，
∵|
AD
|=1，
∴
AC
•
AD
=|
AC
|cos∠DAC，
∵∠BAC=
π
2
+∠DAC，
∴cos∠DAC=sin∠BAC，
∴
AC
•
AD
=|
AC
|cos∠DAC=|
AC
|sin∠BAC，
在△ABC中，由正弦定理得
|
AC
|
sinB
=
|
BC
|
sin∠BAC
，
变形得|
AC
|sin∠BAC=|
BC
|sinB，
∴
AC
•
AD
=|
AC
|cos∠DAC=|
AC
|sin∠BAC
=|
BC
|sinB=|
BC
|•
|
AD
|
|
BD
|
=
3
．
故答案为：
3
．
点评：本题考查向量的数量积的定义和性质，同时考查诱导公式和正弦定理的运用，属于中档题．
练习册系列答案
相关题目
已知函数y=ax（a＞0且a≠1）在[1，2]上的最大值与最小值之和为6，记f（x）=
ax-1
ax+1
．
（1）求a的值；
（2）判断函数f（x）的奇偶性；
（3）求不等式f（x）＞
15
17
的解集．
定义
a
*
b
=|a|×|b|sinθ，θ为
a
与
b
的夹角，已知点A（-3，2），点B（2，3），O是坐标原点，则
OA
*
OB
等于（　　）
A、5B、13C、0D、-2
设函数f（x）的定义域为D，若存在非零实数h使得对于任意x∈M（M⊆D），有x+h∈M，且f（x+h）≥f（x），则称f（x）为M上的h高调函数．现给出下列命题：
①函数f（x）=（
1
2
）x为R上的1高调函数；
②函数f（x）=sin2x为R上的π高调函数；
③若函数f（x）=x2为[-1，+∞）上的m高调函数，那么实数m的取值范围是[2，+∞）．
④函数f（x）=1g（|x-2|+1）上的2高调函数．
其中正确命题的序号是
 
（写出所有正确命题的序号）．
如图，F1，F2是椭圆C：
x2
a2
+
y2
b2
=1的左右两个焦点，|F1F2|=4，长轴长为6，又A，B分别是椭圆C上位于x轴上方的两点，且满足
AF1
=2
BF2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求直线AF1的方程；
（Ⅲ）求四边形ABF2F1的面积．
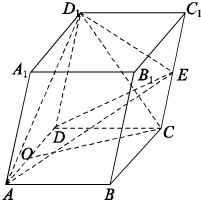已知斜四棱体ABCD-A1B1C1D1各棱长都是2，∠BAD=∠A1AD=60°，E、O分别是棱CC1和棱AD的中点，平面ADD1A1⊥平面ABCD．
（1）求证：OC∥平面AED1；
（2）求二面角E-AD1-D的余弦值．
已知向量
a
=（
3
sinx，cosx），
b
=（cosx，cosx），设函数f（x）=
a
•
b
．
（Ⅰ）求函数f（x）=
a
•
b
的单调增区间；
（Ⅱ）若x∈[-
π
6
，
π
3
]，求函数f（x）=的最值，并指出f（x）取得最值时x的取值．
已知
AB
=（6，1），
BC
=（x，y），
CD
=（-2，-3）
（1）若
BC
∥
DA
，求y=f（x）的解析式
（2）在（1）的条件下，若
AC
⊥
BD
，求x与y的值以及四边形ABCD的面积．
用分析法证明：（
2
+1）2＜
17
5
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网