题目内容
若-3≤log0.5x≤
,求函数f(x)=(log2x-1)•log2
的最大值和最小值.
| 3 |
| 2 |
| x |
| 4 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:利用换元法设t=log2x,将函数转化为关于t的一元二次函数,利用一元二次函数的性质即可得到结论.
解答:
解:(1)∵-3≤log0.5x≤
,
∴-3≤-log2x≤
,
即-
≤log2x≤3,
f(x)=(log2x-1)•log2
=(log2x-1)•(log2x-2),
设t=log2x,则-
≤t≤3,
则函数等价为g(t)=(t-1)•(t-2)=t2-3t+2=(t-
)2-
,
∴当t=
时,函数取得最小值为g(
)=-
,
当t=-
时,函数取得最大值为g(-
)=
.
| 3 |
| 2 |
∴-3≤-log2x≤
| 3 |
| 2 |
即-
| 3 |
| 2 |
f(x)=(log2x-1)•log2
| x |
| 4 |
设t=log2x,则-
| 3 |
| 2 |
则函数等价为g(t)=(t-1)•(t-2)=t2-3t+2=(t-
| 3 |
| 2 |
| 1 |
| 8 |
∴当t=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
当t=-
| 3 |
| 2 |
| 3 |
| 2 |
| 71 |
| 8 |
点评:本题主要考查函数最值的应用,利用对数函数和一元二次函数的性质是解决本题的关键.注意使用换元法.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
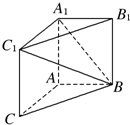 如图,在三棱柱ABCA1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABCA1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.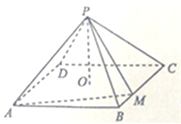 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,PO=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,PO=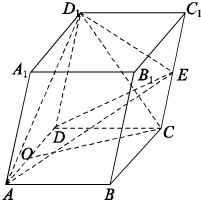 已知斜四棱体ABCD-A1B1C1D1各棱长都是2,∠BAD=∠A1AD=60°,E、O分别是棱CC1和棱AD的中点,平面ADD1A1⊥平面ABCD.
已知斜四棱体ABCD-A1B1C1D1各棱长都是2,∠BAD=∠A1AD=60°,E、O分别是棱CC1和棱AD的中点,平面ADD1A1⊥平面ABCD.