题目内容
过椭圆:
+
=1(a>b>0)的左顶点A且斜率为k的直线交椭圆C于另一点B,F是椭圆的右焦点,BF⊥x轴于F点,当
<k<
时,椭圆的离心率e的取值范围是 .
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| 1 |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:首先利用椭圆的方程与点的位置确定B的坐标进一步确定K的值,最后利用k的范围求出离心率的范围
解答:
解:过椭圆:
+
=1(a>b>0)的左顶点A且斜率为k的直线交椭圆C于另一点B,F是椭圆的右焦点,BF⊥x轴于F点,
则:B(c,
),进一步利用:e=
解得:k=
=1-e,
由于:
<1-e<
,
解得:
<e<
,
故答案为:
<e<
.
| x2 |
| a2 |
| y2 |
| b2 |
则:B(c,
| b2 |
| a |
| c |
| a |
解得:k=
| ||
| a+c |
由于:
| 1 |
| 3 |
| 1 |
| 2 |
解得:
| 1 |
| 2 |
| 2 |
| 3 |
故答案为:
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查的知识要点:点和曲线的位置关系,斜率的求值,离心率的范围.

练习册系列答案
相关题目
椭圆:
+
=1上的一点A关于原点的对称点为B,F2为它的右焦点,若AF2⊥BF2,则三角形△AF2B的面积是( )
| x2 |
| 25 |
| y2 |
| 9 |
A、
| ||
| B、10 | ||
| C、6 | ||
| D、9 |
已知等边△ABC的边长为1,且满足
-2
-3
=
,则
•
=( )
| CP |
| CB |
| CA |
| 0 |
| PA |
| PB |
| A、3 | B、12 | C、-3 | D、-12 |
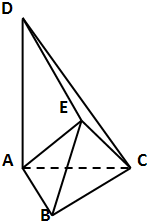 如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2
如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2