题目内容
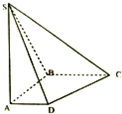 在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=| 1 |
| 2 |
(1)求四棱锥S-ABCD的体积;
(2)求SC与底面ABCD所成角的正切值.
考点:棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)利用四棱锥S-ABCD的体积=
SA•SABCD即可得出.
(2)连接AC,由于SA⊥平面ABCD,可得∠SCA是SC与底面ABCD所成角.在Rt△ABC中,利用勾股定理可得AC=
.在Rt△SAC中,tan∠SCA=
即可得出.
| 1 |
| 3 |
(2)连接AC,由于SA⊥平面ABCD,可得∠SCA是SC与底面ABCD所成角.在Rt△ABC中,利用勾股定理可得AC=
| AB2+BC2 |
| SA |
| AC |
解答:
 解:(1)四棱锥S-ABCD的体积=
解:(1)四棱锥S-ABCD的体积=
SA•SABCD=
×1×
×1=
.
(2)连接AC,∵SA⊥平面ABCD,
∴∠SCA是SC与底面ABCD所成角.
在Rt△ABC中,AC=
=
.
在Rt△SAC中,tan∠SCA=
=
.
 解:(1)四棱锥S-ABCD的体积=
解:(1)四棱锥S-ABCD的体积=| 1 |
| 3 |
| 1 |
| 3 |
1+
| ||
| 2 |
| 1 |
| 4 |
(2)连接AC,∵SA⊥平面ABCD,
∴∠SCA是SC与底面ABCD所成角.
在Rt△ABC中,AC=
| AB2+BC2 |
| 2 |
在Rt△SAC中,tan∠SCA=
| SA |
| AC |
| ||
| 2 |
点评:本题考查了四棱锥的体积、线面角、勾股定理、直角三角形的边角公式,考查了计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x∈R,则
的最大值是( )
| |12cosx-5sinx+39| |
| 13 |
| A、2 | B、4 | C、13 | D、39 |

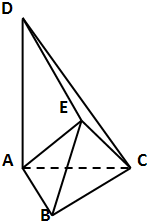 如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2
如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2