题目内容
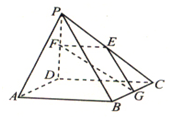 如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.
如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:首先建立空间直角坐标系,进一步求出平面EFG的法向量,再利用
是平面PCD的法向量,利用向量的数量积求出二面角的大小.
| DA |
解答:
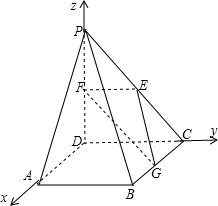 解:建立空间直角坐标系D-xyz,
解:建立空间直角坐标系D-xyz,
则P(0,0,2),C(0,2,0),G(1,2,0),E(0,1,1),F(0,0,1),A(2,0,0).
∴
=(-2,0,2),
=(0,-1,0),
=(1,1,-1)
设平面EFG的法向量为:
=(x,y,z)
所以:
解得:
=(1,0,1)
∵底面ABCD是正方形
∴AD⊥CD
∵PD⊥ABCD
∴AD⊥PD
∴AD⊥平面PCD
∴
是平面PCD的法向量,
=(2,0,0)
所以:cos<
,
>=
=
所以:二面角G-EF-D的大小为45°
 解:建立空间直角坐标系D-xyz,
解:建立空间直角坐标系D-xyz,则P(0,0,2),C(0,2,0),G(1,2,0),E(0,1,1),F(0,0,1),A(2,0,0).
∴
| AP |
| EF |
| EG |
设平面EFG的法向量为:
| n |
所以:
|
解得:
| n |
∵底面ABCD是正方形
∴AD⊥CD
∵PD⊥ABCD
∴AD⊥PD
∴AD⊥平面PCD
∴
| DA |
| DA |
所以:cos<
. |
| DA |
| n |
| ||||
|
|
| ||
| 2 |
所以:二面角G-EF-D的大小为45°
点评:本题考查的知识要点:空间直角坐标系的建立,法向量,向量的数量积,二面角的求法及相关的运算.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
为得到函数y=sin(π-2x)的图象,可以将函数y=sinxcosx-
cos2x+
的图象( )
| 3 |
| ||
| 2 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
