题目内容
9.构造数组,规则如下:第一组是两个1,即(1,1),第二组是(1,2a,1),第三组是(1,a(1+2a),2a,a(2a+1),1)…,在每一组的相邻两个数组之间插入这两个数的和的a倍得到下一组,其中a∈(0,$\frac{1}{4}$),设第n组有an个数,且这an个数的和为Sn(n∈N*).(1)求an和Sn;
(2)求证:$\frac{{a}_{1}-1}{{S}_{1}}$+$\frac{{a}_{2}-1}{{S}_{2}}$+…+$\frac{{a}_{n}-1}{{S}_{n}}$≥$\frac{n}{2}$.
分析 (1)根据数列构造的规则可知an=an-1+(an-1-1)=2an-1-1,即an-1=2(an-1-1).将上式进行迭代,即可得到an-1=2n-1(a1-1)=2n-1.故an=2n-1+1,同理可求出Sn.
(2)令bn=$\frac{{a}_{n}-1}{{S}_{n}}$=$\frac{{2}^{n-1}}{(2a+1)^{n-1}+1}$,利用不等式证明{bn}是递增数列即可得出结论.
解答 解:(1)由题意可知a1=2,当n≥2时,an=an-1+(an-1-1)=2an-1-1,∴an-1=2(an-1-1).
∴an-1=2n-1(a1-1)=2n-1.∴an=2n-1+1.
由数列的构造规则可知S1=2,Sn=Sn-1+2aSn-1-2a=(2a+1)Sn-1-2a,
∴Sn-1=(2a+1)(Sn-1-1)=(2a+1)n-1(S2-1)=(2a+1)n-1,∴Sn=(2a+1)n-1+1.
(2)设bn=$\frac{{a}_{n}-1}{{S}_{n}}$=$\frac{{2}^{n-1}}{(2a+1)^{n-1}+1}$,则bn+1=$\frac{{2}^{n}}{(2a+1)^{n}+1}$,
∵a∈(0,$\frac{1}{4}$),∴1<2a+1<2,∴(2a+1)n<2(2a+1)n-1,∴(2a+1)n+1<2(2a+1)n-1+2,
∴$\frac{{2}^{n}}{(2a+1)^{n}+1}$>$\frac{{2}^{n}}{2(2a+1)^{n-1}+2}$=$\frac{{2}^{n-1}}{(2a+1)^{n-1}+1}$.即bn+1>bn.∴{bn}是递增数列.
∴bn>bn-1>bn-2>…>b2>b1=$\frac{1}{2}$.
∴bn+bn-1+bn-2+…+b2+b1≥$\frac{n}{2}$,即$\frac{{a}_{1}-1}{{S}_{1}}$+$\frac{{a}_{2}-1}{{S}_{2}}$+…+$\frac{{a}_{n}-1}{{S}_{n}}$≥$\frac{n}{2}$.
点评 本题考查了数列的通项公式,递推公式的应用,考查数列与不等式的联系,考查学生分析解决问题的能力,难度较大.

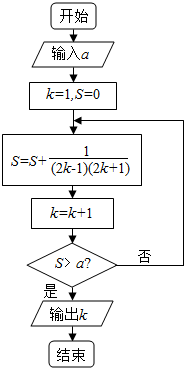 已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )
已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
| A. | (-$\frac{5π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{6}$,0) | D. | (-$\frac{π}{3}$,0) |