题目内容
19.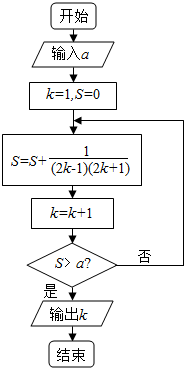 已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )
已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 根据程序框图的流程,计算运行n次的结果,根据输入a=$\frac{9}{19}$,判断n满足的条件,从而求出输出的k值.
解答 解:∵f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,
∴a=f(1)=f(3)=$\frac{9}{19}$.
由程序框图知第一次运行s=0+$\frac{1}{1×3}$,k=2;
第二次运行s=0+$\frac{1}{1×3}$+$\frac{1}{3×5}$,k=3;
…
∴第n次运行s=0+$\frac{1}{1×3}$+$\frac{1}{3×5}$+…+$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$×(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$,
当输入a=$\frac{9}{19}$时,由n>a得n>9,程序运行了10次,输出的k值为11.
故选:C.
点评 本题考查了直到型循环结构的程序框图,由程序框图判断程序运行的功能,用裂项相消法求和是解答本题的关键.

练习册系列答案
相关题目
11.设x0为函数f(x)=sinπx的零点,且满足|x0|+|f(x0+$\frac{1}{2}$)|<33,则这样的零点有( )
| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
 如图,已知圆M:(x-3)2+(y-3)2=4,六边形ABCDEF为圆M的内接正六边形,N为AB的中点,当正六边形ABCDEF绕圆心M转动时,$\overrightarrow{MN}•\overrightarrow{OC}$的最大值是3$\sqrt{6}$.
如图,已知圆M:(x-3)2+(y-3)2=4,六边形ABCDEF为圆M的内接正六边形,N为AB的中点,当正六边形ABCDEF绕圆心M转动时,$\overrightarrow{MN}•\overrightarrow{OC}$的最大值是3$\sqrt{6}$.