题目内容
4.将函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位后,得到函数y=cos($\frac{π}{2}$-2x)的图象,则函数y=sin(ωx+φ)的对称中心为( )| A. | (-$\frac{5π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{6}$,0) | D. | (-$\frac{π}{3}$,0) |
分析 由题意得y=sin(ωx-$\frac{πω}{6}$+φ)=cos($\frac{π}{2}$-2x)=sin2x,可解得函数的解析式为y=sin(2x+$\frac{π}{3}$),从而可求其对称中心.
解答 解:由题意得y=sin(ωx+φ)(ω>0)的图象向右平移$\frac{π}{6}$个单位后,
得到函数y=sin(ωx-$\frac{πω}{6}$+φ)=cos($\frac{π}{2}$-2x)=sin2x,
故可解得:ω=2,φ=$\frac{π}{3}$,
故函数y=sin(ωx+φ)的解析式为y=sin(2x+$\frac{π}{3}$),
由2x+$\frac{π}{3}$=kπ,即x=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z,
k=1时,即解得函数的对称中心为($\frac{π}{3}$,0),
故选:B.
点评 本题主要考查了余弦函数的对称性,考查了函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.如果关于x的不等式ax2-丨x+1丨+2a<0的解集为空集,则实数的取值范围是( )
| A. | [$\frac{1+\sqrt{3}}{4}$,+∞) | B. | [2,+∞) | C. | [$\frac{\sqrt{3}-1}{4}$,+∞) | D. | (-∞,2] |
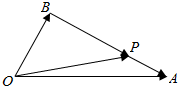 如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.
如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.