题目内容
等比数列的前三项的和为2,前六项的和为6,则其前九项的和为( )
| A、8 | B、10 | C、12 | D、14 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:由题意,S3,S6-S3,S9-S6成等比数列,代入条件,即可求得结论.
解答:
解:∵每相邻两项的和也成等比数列,
∴S3,S6-S3,S9-S6成等比数列,
即2,4,S6-6成等比数列,
∴42=2(S9-6),
∴S9=14.
故选:D.
∴S3,S6-S3,S9-S6成等比数列,
即2,4,S6-6成等比数列,
∴42=2(S9-6),
∴S9=14.
故选:D.
点评:解决此类问题的关键是熟练掌握等比数列的有关性质,并且进行正确的运算.

练习册系列答案
相关题目
已知函数y=2015cos(ωx+φ)(ω>0,0<φ<π),满足f(-x)=-f(x),其图象与直线y=0的某两个交点的横坐标分别为x1,x2,|x1-x2|的最小值为π,则( )
A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
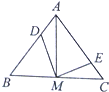 如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=
如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=