题目内容
若f(x)是定义在(0,+∞)上的增函数,且对于x>0满足f(
)=f(x)-f(y).
(1)求f(1)的值;
(2)若f(6)=1,试求解不等式f(x+3)-f(
)<2.
| x |
| y |
(1)求f(1)的值;
(2)若f(6)=1,试求解不等式f(x+3)-f(
| 1 |
| x |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)令x=y=1,能求出f(1).
(2)原不等式可以转化为f(
)<f(6),根据函数的单调性得到关于x的不等式组,解得即可.
(2)原不等式可以转化为f(
| x2+3x |
| 6 |
解答:
解:(1)∵f(
)=f(x)-f(y),
令x=y=1,得f(1)=f(1)-f(1),
∴f(1)=0.
(2)∵f(6)=1,
∴f(x+3)-f(
)<2=f(6)+f(6),
∴f(x2+3x)-f(6)<f(6),
即:f(
)<f(6),
∵f(x)是(0,+∞)上的增函数,
∴
∴解得0<x<
.
故不等式的解集为(0,
).
| x |
| y |
令x=y=1,得f(1)=f(1)-f(1),
∴f(1)=0.
(2)∵f(6)=1,
∴f(x+3)-f(
| 1 |
| x |
∴f(x2+3x)-f(6)<f(6),
即:f(
| x2+3x |
| 6 |
∵f(x)是(0,+∞)上的增函数,
∴
|
∴解得0<x<
-3+3
| ||
| 2 |
故不等式的解集为(0,
-3+3
| ||
| 2 |
点评:本题考查抽象函数的函数值的解法,考查不等式的解法.解题时要认真审题,注意抽象函数的性质的灵活运用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知函数y=2015cos(ωx+φ)(ω>0,0<φ<π),满足f(-x)=-f(x),其图象与直线y=0的某两个交点的横坐标分别为x1,x2,|x1-x2|的最小值为π,则( )
A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
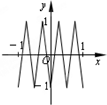
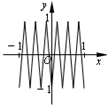
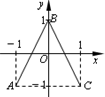 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )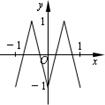
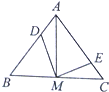 如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=
如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=