题目内容
定义域为[a,b]的函数y=f(x)的图象的两个端点为A、B,M(x,y)是f(x)图象上任意一点,其中x=λa+(1-λ)b(0≤λ≤1),向量
=λ
+(1-λ)
,其中O为坐标原点,若不等式|
|≤k恒成立,则称函数f(x)在[a,b]上“k阶线性近似”.若函数y=x+
在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
| ON |
| OA |
| OB |
| MN |
| 1 |
| x |
A、[
| ||||
B、[
| ||||
| C、[0,+∞) | ||||
| D、[1,+∞) |
考点:平面向量的综合题
专题:平面向量及应用
分析:先得出M、N横坐标相等,再将恒成立问题转化为求函数的最值问题.
解答:
解:由题意,M、N横坐标相等,|
|≤k恒成立,即|
|max≤k,
由N在AB线段上,得A(1,0),B(2,
),
∴直线AB方程为y=
(x+3)
∴|
|═|y1-y2|=|x+
-
(x+3)|=|
+
-
|,
∵
+
≥2
=
,且
+
≤
,
∴|
|=|
+
-
|=
-(
+
)≤
-
,
即|
|的最大值为
-
,
∴k≥
-
.
故选A.
| MN |
| MN |
由N在AB线段上,得A(1,0),B(2,
| 5 |
| 2 |
∴直线AB方程为y=
| 1 |
| 2 |
∴|
| MN |
| 1 |
| x |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
∵
| x |
| 2 |
| 1 |
| x |
|
| 2 |
| x |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
∴|
| MN |
| x |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
| x |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
| 2 |
即|
| MN |
| 3 |
| 2 |
| 2 |
∴k≥
| 3 |
| 2 |
| 2 |
故选A.
点评:本题考查向量知识的运用,考查基本不等式的运用,解答的关键是将已知条件进行转化,同时应注意恒成立问题的处理策略.

练习册系列答案
相关题目
若△ABC满足acosA=bcosB,则△ABC为( )三角形.
| A、等腰 | B、等边 |
| C、等腰直角 | D、等腰或直角 |
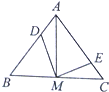 如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=
如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=