题目内容
已知过抛物线y2=4x的焦点F的弦长为36，求弦所在的直线方程．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：弦所在的直线经过焦点（1，0），只需求出直线的斜率，因为弦长为36，所以可以判断直线的斜率是存在的且不为0．
解答：
解：可设弦所在的直线的斜率为k，且与抛物线交于A（x1，y1）、B（x2，y2）两点．
∵抛物线y2=4x的焦点F（1，0），
∴直线方程为y=k（x-1）．
代入抛物线方程，整理得k2x2-（2k2+4）x+k2=0．
∴x1+x2=
，
又AB=AF+BF，抛物线到焦点距离等于到准线距离，
则A到准线距离=x1-（-1）=x1+1，B到准线距离=x2+1，
所以x1+1+x2+1=AF+BF=36，
∴x1+x2=
=34，
解得k=±
，所以所求的直线方程为y=±
（x-1）．
∵抛物线y2=4x的焦点F（1，0），
∴直线方程为y=k（x-1）．
代入抛物线方程，整理得k2x2-（2k2+4）x+k2=0．
∴x1+x2=
| 2k2+4 |
| k2 |
又AB=AF+BF，抛物线到焦点距离等于到准线距离，
则A到准线距离=x1-（-1）=x1+1，B到准线距离=x2+1，
所以x1+1+x2+1=AF+BF=36，
∴x1+x2=
| 2k2+4 |
| k2 |
解得k=±
| ||
| 4 |
| ||
| 4 |
点评：本题考查直线方程的求法，具体涉及到抛物线的简单性质，直线与抛物线的位置关系，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
函数f（x）=sin
x-
+1在区间（0，4）内的零点个数为（ ）
| π |
| 2 |
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
已知正项数列{an}的前n项和为Sn，且a1=1，an=
+
（n≥2），则数列{an}的通项公式为an=（ ）
| Sn |
| Sn+1 |
| A、n-1 | B、n |
| C、2n-1 | D、2n |
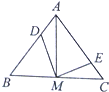如图，在等腰△ABC中，AB=AC，M为BC中点，点D、E分别在边AB、AC上，且AD=