题目内容
已知椭圆C:
+
=1(a>b>0),F1,F2为其左、右焦点,M为椭圆上的一点,△F1F2M的重心为G,内心为I,且直线IG平行x轴,则椭圆的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,设M(x0,y0),由G为△F1MF2的重心,得G点坐标为 G(
,
),利用面积相等可得,
×2c•|y0|=
(2a+2c)|
|,从而求椭圆的离心率.
| x0 |
| 3 |
| y0 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| y0 |
| 3 |
解答:
解:设M(x0,y0),∵G为△F1MF2的重心,
∴G点坐标为 G(
,
),
∵IG∥x轴,
∴I的纵坐标为
,
又∵|MF1|+|MF2|=2a,|F1F2|=2c,
∴S△F1MF2=
•|F1F2|•|y0|,
又∵I为△F1MF2的内心,
∴|
|即为内切圆的半径,
内心I把△F1MF2分为三个底分别为△F1MF2的三边,高为内切圆半径的小三角形,
∴S△F1MF2=
(|MF1|+|F1F2|+|MF2|)|
|,
即
×2c•|y0|=
(2a+2c)|
|,
∴2c=a,
∴椭圆C的离心率为e=
.
故答案为:
.
∴G点坐标为 G(
| x0 |
| 3 |
| y0 |
| 3 |
∵IG∥x轴,
∴I的纵坐标为
| y0 |
| 3 |
又∵|MF1|+|MF2|=2a,|F1F2|=2c,
∴S△F1MF2=
| 1 |
| 2 |
又∵I为△F1MF2的内心,
∴|
| y0 |
| 3 |
内心I把△F1MF2分为三个底分别为△F1MF2的三边,高为内切圆半径的小三角形,
∴S△F1MF2=
| 1 |
| 2 |
| y0 |
| 3 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| y0 |
| 3 |
∴2c=a,
∴椭圆C的离心率为e=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了椭圆的定义及其应用,同时考查了三角形面积相等的应用,属于基础题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知正项数列{an}的前n项和为Sn,且a1=1,an=
+
(n≥2),则数列{an}的通项公式为an=( )
| Sn |
| Sn+1 |
| A、n-1 | B、n |
| C、2n-1 | D、2n |
已知函数y=2015cos(ωx+φ)(ω>0,0<φ<π),满足f(-x)=-f(x),其图象与直线y=0的某两个交点的横坐标分别为x1,x2,|x1-x2|的最小值为π,则( )
A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
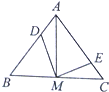 如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=
如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=