题目内容
一个正四棱柱的各个顶点都在一个半径为2cm的球面上,如果正四棱柱的底面边长为2cm,那么该棱柱的表面积为( )
A、(2+4
| ||
B、(4+8
| ||
C、(8+16
| ||
D、(16+32
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:根据几何的性质,求出高的长度,再分别求出各个面的面积,即可求解表面积.
解答:
解:∵一个正四棱柱的各个顶点都在一个半径为2cm的球面上,
正四棱柱的底面边长为2cm,球的直径为正四棱柱的体对角线
∴正四棱柱的体对角线为4,正四棱柱的底面对角线长为2
,
∴正四棱柱的高为
=2
,
∴该棱柱的表面积为2×22+4×2×2
=8+16
,
故选:C
正四棱柱的底面边长为2cm,球的直径为正四棱柱的体对角线
∴正四棱柱的体对角线为4,正四棱柱的底面对角线长为2
| 2 |
∴正四棱柱的高为
| 16-8 |
| 2 |
∴该棱柱的表面积为2×22+4×2×2
| 2 |
| 2 |
故选:C
点评:本题考查了空间简单几何体的棱长,表面积的求解,属于中档题.

练习册系列答案
相关题目
函数f(x)=sin
x-
+1在区间(0,4)内的零点个数为( )
| π |
| 2 |
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
已知正项数列{an}的前n项和为Sn,且a1=1,an=
+
(n≥2),则数列{an}的通项公式为an=( )
| Sn |
| Sn+1 |
| A、n-1 | B、n |
| C、2n-1 | D、2n |
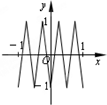
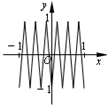
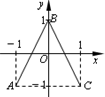 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )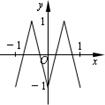
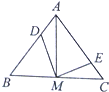 如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=
如图,在等腰△ABC中,AB=AC,M为BC中点,点D、E分别在边AB、AC上,且AD=