题目内容
已知f（a）=
，求f（
）的值．
| sin(π-a)cos(2π-a) |
| cos(-π-a)tana |
| -31π |
| 3 |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由已知得f（a）=
=
=-cosα，由此能求出f（
）的值．
| sin(π-a)cos(2π-a) |
| cos(-π-a)tana |
| sinαcos(-α) |
| -cosαtanα |
| -31π |
| 3 |
解答：
解：∵f（a）=
=
=-cosα，
∴f（
）=-cos（-
）
=-cos（10π+
）
=-cos
=-
．
| sin(π-a)cos(2π-a) |
| cos(-π-a)tana |
=
| sinαcos(-α) |
| -cosαtanα |
=-cosα，
∴f（
| -31π |
| 3 |
| 31π |
| 3 |
=-cos（10π+
| π |
| 3 |
=-cos
| π |
| 3 |
=-
| 1 |
| 2 |
点评：本题考查函数值的求法，是中档题，解题时要认真审题，注意三角函数诱导公式的合理运用．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知直线a过P（0，-1），且与以A（2，3）、B（-3，2）为端点的线段相交，则直线a的斜率k的取值范围是（ ）
| A、（-∞，-1]∪[2，+∞） |
| B、（-∞，-1] |
| C、[2，+∞） |
| D、[-1，2] |
将各项均为正整数的数列{an}排成如图所示的三角形数阵（第n行有n个数；在同一行中，各项的下标从左到右依次增大）．bn表示该数阵中第n行第1个数．已知数列{bn}为公比为q等比数列，a1=1，a3=a2+1，且从第3行开始，从左到右，各行均构成公差为d的等差数列．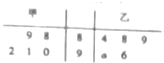
某机械厂今年进行了五次技能考核，其中甲、乙两名技术骨干得分的平均分相等，成绩统计情况如茎叶图所示（其中a是0-9的某个整数