题目内容
以下是用二分法求方程x3+3x-5=0的一个近似解(精确度为0.1)的不完整的过程,请补充完整.
解:设函数f(x)=x3+3x-5,其图象在(-∞,+∞)上是连续不断的,且f(x)在(-∞,+∞)上是单调递 (增或减).
先求f(0)= ,f(1)= ,f(2)= .
所以f(x)在区间 内存在零点x0,再填表:
下结论: .
(可参考条件:f(1.125)<0,f(1.1875)>0;符号填+、-)
解:设函数f(x)=x3+3x-5,其图象在(-∞,+∞)上是连续不断的,且f(x)在(-∞,+∞)上是单调递
先求f(0)=
所以f(x)在区间
下结论:
(可参考条件:f(1.125)<0,f(1.1875)>0;符号填+、-)
| 区间 | 中点m | f(m)符号 | 区间长度 |
考点:二分法求方程的近似解
专题:计算题,作图题,函数的性质及应用
分析:由函数y=x3与y=3x-5在(-∞,+∞)上都是增函数可知f(x)在(-∞,+∞)上是单调递增的,求函数值,从而得到f(x)在区间(1,2)内存在零点x0,利用二分法完成表格后下结论即可.
解答:
解:设函数f(x)=x3+3x-5,
∵函数y=x3与y=3x-5在(-∞,+∞)上都是增函数,
∴f(x)在(-∞,+∞)上是单调递增的,
又∵f(0)=0+0-5=-5,
f(1)=1+3-5=-1,
f(2)=8+6-5=9,
∴f(x)在区间(1,2)内存在零点x0,
利用二分法可得下表,
方程x3+3x-5=0在精确度为0.1的要求下的一个近似值为1.125.
故答案为:增,-5,-1,9,(1,2),方程x3+3x-5=0在精确度为0.1的要求下的一个近似值为1.125.
∵函数y=x3与y=3x-5在(-∞,+∞)上都是增函数,
∴f(x)在(-∞,+∞)上是单调递增的,
又∵f(0)=0+0-5=-5,
f(1)=1+3-5=-1,
f(2)=8+6-5=9,
∴f(x)在区间(1,2)内存在零点x0,
利用二分法可得下表,
| 区间 | 中点m | f(m)的符号 | 区间长度 |
| (1,2) | 1.5 | + | 1 |
| (1,1.5) | 1.25 | + | 0.5 |
| (1,1.25) | 1.125 | - | 0.25 |
| (1.125,1.25) | 1.1875 | + | 0.125 |
| (1.125,1.1875) | 0.0625 |
故答案为:增,-5,-1,9,(1,2),方程x3+3x-5=0在精确度为0.1的要求下的一个近似值为1.125.
点评:本题考查了二分法求方程的近似解的过程,属于基础题.

练习册系列答案
相关题目
函数f(x)=
的定义域为( )
| 1 | ||
|
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、(-∞,-1) |
| D、(-1,+∞) |
如图执行下面的流程图,那么输出的S等于( )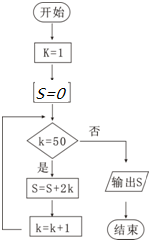

| A、2450 | B、2500 |
| C、2550 | D、2652 |
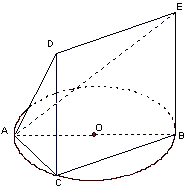 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,DC=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,DC=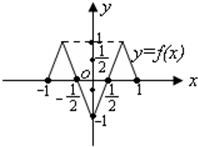 已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是
已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是