题目内容
已知A、B、C是直线l上的三点,向量
,
,
满足
=m2
+n2
,则
+
的取值范围是 .
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| m2 |
| 1+n2 |
| n2 |
| 1+m2 |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:先根据题意得出m2+n2=1,从而
+
=2(
+
)-2,令sinα=m,cosα=n,令y=2(
+
)-2,通过三角函数的性质,从而得出答案.
| m2 |
| 1+n2 |
| n2 |
| 1+m2 |
| 1 |
| 1+n2 |
| 1 |
| 1+m2 |
| 1 |
| 1+n2 |
| 1 |
| 1+m2 |
解答:
解:∵A、B、C是直线l上的三点,
向量
,
,
满足
=m2
+n2
,
∴m2+n2=1,
∴
+
=
+
=2(
+
)-2,
令sinα=m,cosα=n,令y=2(
+
)-2,
∴y=2(
+
)-2
=2•
-2
=
-2,
当sin2α=1时,y=
,当sin2α=-1时,y=
,
∴
≤y≤
,
故答案为:[
,
].
向量
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
∴m2+n2=1,
∴
| m2 |
| 1+n2 |
| n2 |
| 1+m2 |
| 2-(1+n2) |
| 1+n2 |
| 2-(1+m2) |
| 1+m2 |
| 1 |
| 1+n2 |
| 1 |
| 1+m2 |
令sinα=m,cosα=n,令y=2(
| 1 |
| 1+n2 |
| 1 |
| 1+m2 |
∴y=2(
| 1 |
| 1+cos2α |
| 1 |
| 1+sin2α |
=2•
| 1+sin2α+1+cos2α |
| (1+sin2α)(1+cos2α) |
=
| 6 | ||
2+
|
当sin2α=1时,y=
| 2 |
| 3 |
| 10 |
| 7 |
∴
| 2 |
| 3 |
| 10 |
| 7 |
故答案为:[
| 2 |
| 3 |
| 10 |
| 7 |
点评:本题考查了平面向量基本定理,考查转化思想,考查三角函数的性质,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线3x+4y-13=0与圆x2+y2-4x-6y+12=0的位置关系是( )
| A、相离 | B、相交 |
| C、相切 | D、无法判定 |
如图执行下面的流程图,那么输出的S等于( )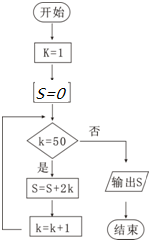

| A、2450 | B、2500 |
| C、2550 | D、2652 |
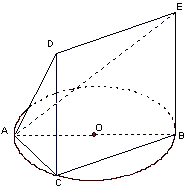 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,DC=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,DC=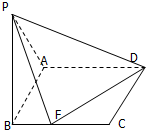 如图,已知平面PAB⊥平面ABCD,且四边形ABCD是矩形,AD:AB=3:2,△PAB为等边三角形,F是线段BC上的点且满足CF=2BF.
如图,已知平面PAB⊥平面ABCD,且四边形ABCD是矩形,AD:AB=3:2,△PAB为等边三角形,F是线段BC上的点且满足CF=2BF.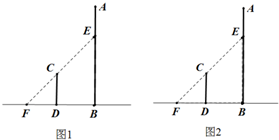 某公司为了公司周年庆典,现将公司门前广场进行装饰,广场上有一垂直于地面的墙面AB高为8+8
某公司为了公司周年庆典,现将公司门前广场进行装饰,广场上有一垂直于地面的墙面AB高为8+8