题目内容
函数y=ln（1+
）+
的定义域为 ．
| 1 |
| x |
| 1-x |
考点：函数的定义域及其求法
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：根据对数函数和二次根式的性质，要使函数有意义，则需真数大于零且被开方式非负．
解答：
解：由
，
即有
，
则0＜x≤1或x＜-1．
则定义域为（0，1]∪（-∞，-1）．
故答案为：（0，1]∪（-∞，-1）．
|
即有
|
则0＜x≤1或x＜-1．
则定义域为（0，1]∪（-∞，-1）．
故答案为：（0，1]∪（-∞，-1）．
点评：本题主要考查对数函数和二次根式的定义域，基本求法是真数大于零且被开方式非负．要注意定义域要写成集合或区间的形式．
练习册系列答案
考前必练系列答案
相关题目
直线3x+4y-13=0与圆x2+y2-4x-6y+12=0的位置关系是（ ）
| A、相离 | B、相交 |
| C、相切 | D、无法判定 |
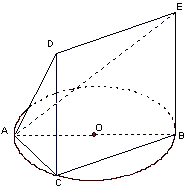如图，△ABC内接于圆O，AB是圆O的直径，AB=2，BC=1，DC=
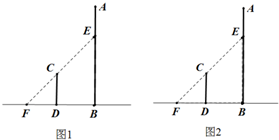某公司为了公司周年庆典，现将公司门前广场进行装饰，广场上有一垂直于地面的墙面AB高为8+8