题目内容
二次函数f（x）=x2-16x+q+3．若函数在区间[-1，1]上存在零点，求实数q的取值范围．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：由二次函数的单调性易得
，解关于q的不等式组可得．
|
解答：
解：∵二次函数f（x）=x2-16x+q+3的对称轴为x=8，
∴函数f（x）在区间[-1，1]上是减函数，
∵函数在区间[-1，1]上存在零点，
∴必有
，即
，
解不等式组可得-20≤q≤12，
∴实数q的取值范围为[-20，12]
∴函数f（x）在区间[-1，1]上是减函数，
∵函数在区间[-1，1]上存在零点，
∴必有
|
|
解不等式组可得-20≤q≤12，
∴实数q的取值范围为[-20，12]
点评：本题考查二次函数的零点分布，得出q的不等式组是解决问题的关键，属基础题．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
“a＜-4”是函数f（x）=ax+3在[-1，1]上存在零点的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
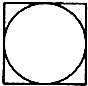如图是一个边长为1的正方形及其内切圆，现随机地向该正方形内投一粒黄豆（视为一点），则黄豆落入圆内的概率为已知a，b是实数，则“|a-b|=|a|-|b|”是“ab＞0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |