题目内容
已知圆C:x2+y2-2x-4y-12=0和点A(3,0),直线l过点A与圆交于P,Q两点.
(1)若以PQ为直径的圆的面积最大,求直线l的方程;
(2)若以PQ为直径的圆过原点,求直线l的方程.
(1)若以PQ为直径的圆的面积最大,求直线l的方程;
(2)若以PQ为直径的圆过原点,求直线l的方程.
考点:直线与圆的位置关系
专题:综合题,直线与圆
分析:(1)以PQ为直径的圆的面积最大,则直线l过圆心,即可求直线l的方程;
(2)若以PQ为直径的圆过原点,利用圆系方程,即可求直线l的方程.
(2)若以PQ为直径的圆过原点,利用圆系方程,即可求直线l的方程.
解答:
解:(1)圆C:x2+y2-2x-4y-12=0可化为圆C:(x-1)2+(y-2)2=17,圆心为(1,2),
∵以PQ为直径的圆的面积最大,
∴直线l过点(1,2),
∵直线l过A(3,0),
∴直线l的方程为x+y-3=0;
(2)设直线l的方程为y=k(x-3),以PQ为直径的圆的方程为x2+y2-2x-4y-12+λ(kx-y-3k)=0
(0,0)代入圆,整理可得-12-3λk=0,①
圆心坐标为(1-
,2+
),代入y=k(x-3),可得2+
=k(1-
-3),②
由①②可得λ=-1,k=4,
∴直线l的方程为y=4(x-3).
∵以PQ为直径的圆的面积最大,
∴直线l过点(1,2),
∵直线l过A(3,0),
∴直线l的方程为x+y-3=0;
(2)设直线l的方程为y=k(x-3),以PQ为直径的圆的方程为x2+y2-2x-4y-12+λ(kx-y-3k)=0
(0,0)代入圆,整理可得-12-3λk=0,①
圆心坐标为(1-
| λk |
| 2 |
| λ |
| 2 |
| λ |
| 2 |
| λk |
| 2 |
由①②可得λ=-1,k=4,
∴直线l的方程为y=4(x-3).
点评:本题考查直线方程,考查直线与圆的位置关系,考查圆系方程,正确运用圆系方程,减少计算量.

练习册系列答案
相关题目
设a=
dx,则二项式(ax-
)8的展开式中x2项的系数是( )
| ∫ | e e-1 |
| 1 |
| x |
| 1 | ||
|
| A、-1120 | B、1120 |
| C、-1792 | D、1792 |
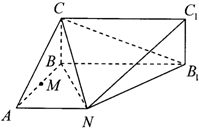 已知矩形BCC1B1所在平面与平面ABB1N垂直,AN∥BB1,AB⊥BB1,且BB1=8,AN=AB=BC=4,
已知矩形BCC1B1所在平面与平面ABB1N垂直,AN∥BB1,AB⊥BB1,且BB1=8,AN=AB=BC=4,