题目内容

已知两个单位向量
a
与
b
的夹角为
π
3
，若（
a
+λ
b
）⊥（λ
a
-
b
），则λ=
 
．
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的数量积的定义和向量垂直的条件：数量积为0，解方程即可得到．
解答： 解：两个单位向量
a
与
b
的夹角为
π
3
，
则
a
•
b
=1×1×cos
π
3
=
1
2
，
若（
a
+λ
b
）⊥（λ
a
-
b
），
则（
a
+λ
b
）•（λ
a
-
b
）=0，
即有λ
a
2-λ
b
2+（λ2-1）
a
•
b
=0，
即λ-λ+
1
2
（λ2-1）=0，
解得λ=±1．
故答案为：-1或1．
点评：本题考查向量的数量积的定义和性质，主要考查向量垂直的条件，考查运算能力，属于基础题．
练习册系列答案
相关题目
设随机变量ξ～N（μ，?2），且P（ξ＜-1）=P（ξ＞2）=0.3，则P=（-2＜ξ＜0）=
 
．
求函数y=
cosx-
1
2
的定义域．
已知x，y，z∈R，且x-2y+2z=5，则（x+5）2+（y-1）2+（z+3）2的最小值是
 
．
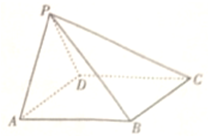已知四棱锥P-ABCD，侧面PAD⊥底面ABCD，侧面PAD为等边三角形，底面ABCD为棱形且∠DAB=
π
3
．
（Ⅰ）求证：PB⊥AD；
（Ⅱ）求平面PAB与平面PCD所成的角（锐角）的余弦值．
已知向量
a
=（cos
x
2
，1），
b
=（
3
sin
x
2
，cos2
x
2
），函数f（x）=
a
•
b
．
（1）求函数f（x）的最小正周期及单调递增区间；
（2）若f（x）=1，求cos（
2π
3
-2x）的值．
如图，M、N是焦点为F的抛物线y2=2px（p＞0）上两个不同的点，且线段MN中点A的横坐标为4-
p
2
，
（1）求|MF|+|NF|的值；
（2）若p=2，直线MN与x轴交于点B点，求点B横坐标的取值范围．
已知函数f（x）=msinx-cosx，若x0是函数f（x）的一个极值点，且cos2x0=-
3
5
，则m的值为（　　）
A、1B、±1C、2D、±2
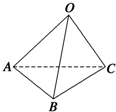如图所示，已知空间四边形OABC中，OB=OC，且∠AOB=∠AOC=
π
3
，则cos＜
OA
，
BC
＞的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网