Question

7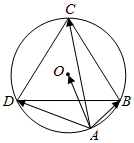．如图，设正△BCD的外接圆O的半径为R（$\frac{1}{2}$＜R＜$\frac{\sqrt{3}}{3}$），点A在BD下方的圆弧上，则（$\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$）•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$．

Answer 1

分析 先根据三角形为正三角形，再设∠CAO=θ，得到AC=2Rcosθ，根据向量的数量的运算得到（$\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$）•$\overrightarrow{AC}$得到2R²cos²θ-2Rcosθ，再构造函数y=2t²-2t=2（t-$\frac{1}{2}$）²-$\frac{1}{2}$，即可求出最值．

解答 解：∵△BCD为正三角形，
∴∠CAD=∠CAB=∠DAB=∠CBD=60°，
设∠CAO=θ，
∴AC=2Rcosθ，
∴（$\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$）•$\overrightarrow{AC}$=$\overrightarrow{AO}$•$\overrightarrow{AC}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\overrightarrow{AC}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$$•\overrightarrow{AC}$=2R²cos²θ-$\frac{1}{2}$×2Rcosθ-$\frac{1}{2}$×2Rcosθ=2R²cos²θ-2Rcosθ，
设Rcosθ=t，
∵$\frac{1}{2}$＜R＜$\frac{\sqrt{3}}{3}$，0°≤θ＜60°，即$\frac{1}{2}$＜cosθ≤1，
∴$\frac{1}{4}$＜t＜$\frac{\sqrt{3}}{3}$
则y=2t²-2t=2（t-$\frac{1}{2}$）²-$\frac{1}{2}$
∴当t=$\frac{1}{2}$，y有最小值，即为-$\frac{1}{2}$，
故答案为：-$\frac{1}{2}$．

点评 本题考查了向量的数量积 的运算以及函数的最值问题，关键是转化，掌握单位向量的概念，属于中档题．