题目内容
19.已知sinθ=$\frac{3}{5}$,θ∈($\frac{π}{2}$,π),求cos(2θ-$\frac{2}{3}$π)的值.分析 利用同角三角函数基本关系式以及两角和与差的余弦函数,二倍角公式化简求解即可.
解答 解:sinθ=$\frac{3}{5}$,θ∈($\frac{π}{2}$,π),
可得cosθ=-$\frac{4}{5}$,
cos(2θ-$\frac{2}{3}$π)=-$\frac{1}{2}$cos2θ+$\frac{\sqrt{3}}{2}$sin2θ=-$\frac{1}{2}$cos2θ+$\sqrt{3}$sinθcosθ+$\frac{1}{2}$=$-\frac{1}{2}×(-\frac{4}{5})^{2}$-$\sqrt{3}×$$\frac{3}{5}$×$\frac{4}{5}$+$\frac{1}{2}$
=$\frac{17-24\sqrt{3}}{50}$.
点评 本题考查同角三角函数基本关系式以及两角和与差的余弦函数,二倍角公式的应用,考查计算能力.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
9.设三条不同的直线分别为m,n,l,两个不同的平面分别为α,β.则下列说法正确的是( )
| A. | 若m∥n,n?α,则m∥α | |
| B. | 若m,n为异面直线,且m?α,n?β,则α∥β | |
| C. | 若m⊥n,α⊥β,m⊥α,则n⊥β | |
| D. | 若m∥α,m∥β,α∩β=l,则m∥l |
14.在△ABC中,若a=$\sqrt{2}$,c=2,A=30°,则C等于( )
| A. | 30° | B. | 30°或150° | C. | 45° | D. | 45°或135° |
4.已知函数f(x)=2sinωxcosωx-2$\sqrt{3}$cos2ωx相邻对称轴之间的距离为$\frac{π}{2}$,则下列结论中错误的是( )
| A. | f(x)在区间(0,$\frac{π}{4}$)上单调递增 | |
| B. | f(x)的一个对称中心为($\frac{π}{6}$,-$\sqrt{3}$) | |
| C. | 当x∈[0,$\frac{π}{2}$]时,f(x)的值域为[-2$\sqrt{3}$,0] | |
| D. | 将f(x)的纵坐标不变,横坐标缩短为原来的$\frac{1}{2}$,再向左平移$\frac{π}{6}$个单位后得到y=2sin(4x+$\frac{π}{3}$)-$\sqrt{3}$ |
7.某校三年级在5月份进行一次质量考试,考生成绩情况如图所示某校高三年级在5月份进行一次质量考试,考生成绩情况如表所示:
已知用分层抽样方法在不低于550分的考生中随机抽取5名考生进行质量分析,其中文科考生抽取了2名.
(1)已知该校不低于480分的文科理科考生人数之比为1:2,不低于400分的文科理科考生人数之比为2:5,求x、y的值.
(2)用分层抽样的方法在不低于550分考生中随机抽取5名考生,从这5名考生汇总抽取2名学生进行调查,求至少有一名文科生的概率.
| [0,400) | [400,480) | [480,550) | [550,750) | |
| 文科考生 | 67 | 35 | 19 | 6 |
| 理科考生 | 53 | x | y | z |
(1)已知该校不低于480分的文科理科考生人数之比为1:2,不低于400分的文科理科考生人数之比为2:5,求x、y的值.
(2)用分层抽样的方法在不低于550分考生中随机抽取5名考生,从这5名考生汇总抽取2名学生进行调查,求至少有一名文科生的概率.
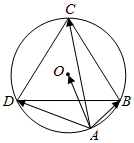 如图,设正△BCD的外接圆O的半径为R($\frac{1}{2}$<R<$\frac{\sqrt{3}}{3}$),点A在BD下方的圆弧上,则($\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$)•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$.
如图,设正△BCD的外接圆O的半径为R($\frac{1}{2}$<R<$\frac{\sqrt{3}}{3}$),点A在BD下方的圆弧上,则($\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$)•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$.