题目内容
18．在△ABC中，设a=20，b=29，c=21，求这个三角形的最大角．分析 利用大边对大角得到B为最大角，利用余弦定理表示出cosB，将三边长代入求出cosB的值，即可确定出B的度数．
解答 解：判断得到B为最大角，
∵在△ABC中，a=20，b=29，c=21，
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{2{0}^{2}+2{1}^{2}-2{9}^{2}}{2×20×21}$=0，
则B=90°，
故这个三角形的最大角为90°．
点评 此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键，属于基础题．
练习册系列答案
相关题目
9．设三条不同的直线分别为m，n，l，两个不同的平面分别为α，β．则下列说法正确的是（ ）
| A． | 若m∥n，n?α，则m∥α | |
| B． | 若m，n为异面直线，且m?α，n?β，则α∥β | |
| C． | 若m⊥n，α⊥β，m⊥α，则n⊥β | |
| D． | 若m∥α，m∥β，α∩β=l，则m∥l |
13．函数y=sin$\frac{x}{2}$sin（$\frac{π}{2}-\frac{x}{2}$）的最小正周期是（ ）
| A． | 4π | B． | 2π | C． | π | D． | $\frac{π}{2}$ |
3．函数f（x）=x2-1的单调递减区间为（ ）
| A． | [0，+∞） | B． | （-∞，0] | C． | [-1，+∞） | D． | （-∞，-1] |
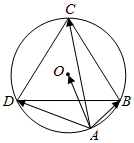如图，设正△BCD的外接圆O的半径为R（$\frac{1}{2}$＜R＜$\frac{\sqrt{3}}{3}$），点A在BD下方的圆弧上，则（$\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$）•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$．