题目内容
15.对于函数f(x),g(x)满足:对任意x∈R,都有f(x2-2x+3)=g(x),若关于x的方程g(x)+sin$\frac{π}{2}$x=0只有5个根,则这5个根之和为( )| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
分析 根据条件,先判断g(x)关于x=1对称,然后利用函数与方程之间的关系转化为两个函数的交点问题进行求解即可.
解答  解:∵y=x2-2x+3的对称轴为x=1,
解:∵y=x2-2x+3的对称轴为x=1,
∴由f(x2-2x+3)=g(x)得g(x)关于x=1对称
由g(x)+sin$\frac{π}{2}$x=0得g(x)=-sin$\frac{π}{2}$x,
作出函数y=-sin$\frac{π}{2}$x的图象,
若程g(x)+sin$\frac{π}{2}$x=0只有5个根,
则其中一个根x=1,其余四个根两两关于x=1对称,
则关于对称的根分别为x1,和x2,x3和x4,
则$\frac{{x}_{1}+{x}_{2}}{2}=1$,$\frac{{x}_{3}+{x}_{4}}{2}=1$,
则x1+x2=2,x3+x4=2,
则这5个根之和为2+2+1=5,
故选:A.
点评 本题主要考查根的个数的判断,根据条件判断两个函数的对称性是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
7.某校三年级在5月份进行一次质量考试,考生成绩情况如图所示某校高三年级在5月份进行一次质量考试,考生成绩情况如表所示:
已知用分层抽样方法在不低于550分的考生中随机抽取5名考生进行质量分析,其中文科考生抽取了2名.
(1)已知该校不低于480分的文科理科考生人数之比为1:2,不低于400分的文科理科考生人数之比为2:5,求x、y的值.
(2)用分层抽样的方法在不低于550分考生中随机抽取5名考生,从这5名考生汇总抽取2名学生进行调查,求至少有一名文科生的概率.
| [0,400) | [400,480) | [480,550) | [550,750) | |
| 文科考生 | 67 | 35 | 19 | 6 |
| 理科考生 | 53 | x | y | z |
(1)已知该校不低于480分的文科理科考生人数之比为1:2,不低于400分的文科理科考生人数之比为2:5,求x、y的值.
(2)用分层抽样的方法在不低于550分考生中随机抽取5名考生,从这5名考生汇总抽取2名学生进行调查,求至少有一名文科生的概率.
4.已知$sin({65°+α})=\frac{1}{3}$,则cos(25°-α)的值为( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
5.若复数z满足$\frac{z+2i}{z}$=2+3i,其中i为虚数单位,则z=( )
| A. | $\frac{2}{5}$+$\frac{3}{5}$i | B. | $\frac{3}{5}$+$\frac{2}{5}$i | C. | $\frac{3}{5}$+$\frac{1}{5}$i | D. | $\frac{1}{5}$+$\frac{3}{5}$i |
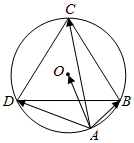 如图,设正△BCD的外接圆O的半径为R($\frac{1}{2}$<R<$\frac{\sqrt{3}}{3}$),点A在BD下方的圆弧上,则($\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$)•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$.
如图,设正△BCD的外接圆O的半径为R($\frac{1}{2}$<R<$\frac{\sqrt{3}}{3}$),点A在BD下方的圆弧上,则($\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$)•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$.