题目内容
17.已知等差数列{an}的前n项和为Sn,且a3=6,S7=56,数列{bn}前n项和为Tn,且2Tn-3bn+2=0.(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设${c_n}=\left\{{\begin{array}{l}{{a_n},n为奇数}\\{{b_n},n为偶数}\end{array}}\right.$,求数列{cn}的前n项和Qn.
分析 (I)设等差数列{an}的公差为d,由于a3=6,S7=56,可得$\left\{\begin{array}{l}{{a}_{1}+2d=6}\\{7{a}_{1}+\frac{7×6}{2}d=56}\end{array}\right.$,解出即可得出.由数列{bn}前n项和为Tn,且2Tn-3bn+2=0.利用递推关系即可得出.
(II)对n分类讨论,分别利用等差数列与等比数列的前n项和公式即可得出.
解答 解:(I)设等差数列{an}的公差为d,∵a3=6,S7=56,
∴$\left\{\begin{array}{l}{{a}_{1}+2d=6}\\{7{a}_{1}+\frac{7×6}{2}d=56}\end{array}\right.$,解得a1=d=2.
∴an=2+2(n-1)=2n.
∵数列{bn}前n项和为Tn,且2Tn-3bn+2=0.
∴2b1-3b1+2=0,解得b1=2.
当n≥2时,2Tn-1-3bn-1+2=0,
∴2bn-3bn+3bn-1=0,
∴bn=3bn-1,
∴数列{bn}是等比数列,首项为2,公比为3.
∴bn=2×3n-1.
(II)${c_n}=\left\{{\begin{array}{l}{{a_n},n为奇数}\\{{b_n},n为偶数}\end{array}}\right.$,
当n=2k-1(k∈N*)时,数列{cn}的前n项和Qn=(a1+a3+…+a2k-1)+(b2+b4+…+b2k-2)
=2[1+3+…+(2k-1)]+2×(3+33+…+32k-3)
=$2×\frac{k(1+2k-1)}{2}$+2×$\frac{3({9}^{k-1}-1)}{9-1}$
=2k2+$\frac{3}{4}({9}^{k-1}-1)$
=$2×(\frac{n+1}{2})^{2}$+$\frac{3}{4}×({9}^{\frac{n-1}{2}}-1)$.
当n=2k(k∈N*)时,数列{cn}的前n项和Qn=(a1+a3+…+a2k-1)+(b2+b4+…+b2k)
=2[1+3+…+(2k-1)]+2×(3+33+…+32k-1)
=2k2+$2×\frac{3({9}^{k}-1)}{9-1}$
=$\frac{{n}^{2}}{2}$+$\frac{3}{4}({9}^{\frac{n}{2}}-1)$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.

| A. | 若m∥n,n?α,则m∥α | |
| B. | 若m,n为异面直线,且m?α,n?β,则α∥β | |
| C. | 若m⊥n,α⊥β,m⊥α,则n⊥β | |
| D. | 若m∥α,m∥β,α∩β=l,则m∥l |
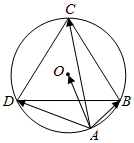 如图,设正△BCD的外接圆O的半径为R($\frac{1}{2}$<R<$\frac{\sqrt{3}}{3}$),点A在BD下方的圆弧上,则($\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$)•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$.
如图,设正△BCD的外接圆O的半径为R($\frac{1}{2}$<R<$\frac{\sqrt{3}}{3}$),点A在BD下方的圆弧上,则($\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$)•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$.