题目内容
12.在△ABC中,若已知AC=10,BC=15和A=60°,则sinB=$\frac{\sqrt{3}}{3}$.分析 由已知利用正弦定理即可计算得解.
解答 解:在△ABC中,∵AC=10,BC=15和A=60°,
∴由正弦定理可得:sinB=$\frac{AC•sinA}{BC}$=$\frac{10×\frac{\sqrt{3}}{2}}{15}$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题主要考查了正弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
3.函数f(x)=x2-1的单调递减区间为( )
| A. | [0,+∞) | B. | (-∞,0] | C. | [-1,+∞) | D. | (-∞,-1] |
17.在△ABC中,若b2-c2-a2=-ac,则B等于( )
| A. | 120° | B. | 30°或150° | C. | 45° | D. | 60° |
4.已知函数f(x)=2sinωxcosωx-2$\sqrt{3}$cos2ωx相邻对称轴之间的距离为$\frac{π}{2}$,则下列结论中错误的是( )
| A. | f(x)在区间(0,$\frac{π}{4}$)上单调递增 | |
| B. | f(x)的一个对称中心为($\frac{π}{6}$,-$\sqrt{3}$) | |
| C. | 当x∈[0,$\frac{π}{2}$]时,f(x)的值域为[-2$\sqrt{3}$,0] | |
| D. | 将f(x)的纵坐标不变,横坐标缩短为原来的$\frac{1}{2}$,再向左平移$\frac{π}{6}$个单位后得到y=2sin(4x+$\frac{π}{3}$)-$\sqrt{3}$ |
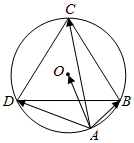 如图,设正△BCD的外接圆O的半径为R($\frac{1}{2}$<R<$\frac{\sqrt{3}}{3}$),点A在BD下方的圆弧上,则($\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$)•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$.
如图,设正△BCD的外接圆O的半径为R($\frac{1}{2}$<R<$\frac{\sqrt{3}}{3}$),点A在BD下方的圆弧上,则($\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$)•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$.