题目内容
16.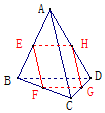 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,(1)求证四边形EFGH是平行四边
(2)若AC⊥BD时,求证:EFGH为矩形.
分析 (1)利用三角形的中位线定理、平行四边形的判定定理可得:四边形EFGH是平行四边形.
(2)由EF∥AC,EH∥BD,AC⊥BD可得EF⊥EH.即可证明平行四边形EFGH是矩形.
解答  (1)证明:连结AC,BD,
(1)证明:连结AC,BD,
∵E,F是△ABC的边AB,BC上的中点,
∴EF∥AC,
同理,HG∥AC,
∴EF∥HG,
同理,EH∥FG,
∴四边形EFGH是平行四边;
(2)证明:由(1)四边形EFGH是平行四边形.
∵EF∥AC,EH∥BD,
∴由AC⊥BD得,EF⊥EH,
∴EFGH为矩形.
点评 本题考查了三角形的中位线定理、平行四边形的判定、矩形的判定定理,考查了推理能力,属于基础题.

练习册系列答案
相关题目
6.将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论,其中错误的结论是( )
| A. | AC⊥BD | B. | △ACD是等边三角形 | ||
| C. | .AB与CD所成的角为60° | D. | AB与平面BCD所成的角为60° |
7.若函数f(x)的定义域为[-1,5],则函数f(2x+1)的定义域为( )
| A. | [-1,11] | B. | [-1,5] | C. | [-1,2] | D. | [-2,4] |
4.若A、B是锐角三角形△ABC的两个内角,如果点P的坐标为P(cosB-sinA,sinB-cosA),则点P在直角坐标平面内位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限t |
5.已知函数f(x)=2exln$\sqrt{e}$-kx(e=2.17128…是自然对数的底数)有两个不同的零点,则实数k的取值范围是( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (e,+∞) | D. | (1,+∞) |