题目内容
4.若A、B是锐角三角形△ABC的两个内角,如果点P的坐标为P(cosB-sinA,sinB-cosA),则点P在直角坐标平面内位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限t |
分析 由A,B为锐角三角形的两个内角,知A+B>$\frac{π}{2}$,所以cosB-sinA<0,同理可得sinB-cosA>0,由此能求出点P所在的象限.
解答 解:∵A,B为锐角三角形的两个内角,
∴A+B>$\frac{π}{2}$,
∴A>$\frac{π}{2}$-B>0,
∴sinA>sin($\frac{π}{2}$-B)=cosB,
∴cosB-sinA<0,
同理可得sinB-cosA>0,
故选B.
点评 本题考查三角函数值的符号,解题时要认真审题,仔细解答.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.若a>b,则下列正确的是( )
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
| A. | 4 | B. | 2,3 | C. | 1,4 | D. | 1,2,3,4 |
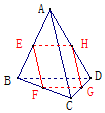 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,